Reviewers: buda Reviewed By: buda Differential Revision: https://phabricator.memgraph.io/D1532
157 lines
7.3 KiB
Markdown
157 lines
7.3 KiB
Markdown
# Graph Algorithms
|
|
|
|
## Introduction
|
|
|
|
The graph is a mathematical structure used to describe a set of objects in which
|
|
some pairs of objects are "related" in some sense. Generally, we consider
|
|
those objects as abstractions named `nodes` (also called `vertices`).
|
|
Aforementioned relations between nodes are modelled by an abstraction named
|
|
`edge` (also called `relationship`).
|
|
|
|
It turns out that a lot of real-world problems can be successfully modeled
|
|
using graphs. Some natural examples would contain railway networks between
|
|
cities, computer networks, piping systems and Memgraph itself.
|
|
|
|
This article outlines some of the most important graph algorithms
|
|
that are internally used by Memgraph. We believe that advanced users could
|
|
significantly benefit from obtaining basic knowledge about those algorithms.
|
|
The users should also note that this article does not contain an in-depth
|
|
analysis of algorithms and their implementation details since those are
|
|
well documented in the appropriate literature and, in our opinion, go well out
|
|
of scope for user documentation. That being said, we will include the relevant
|
|
information for using Memgraph effectively and efficiently.
|
|
|
|
Contents of this article include:
|
|
|
|
* [Breadth First Search (BFS)](#breadth-first-search)
|
|
* [Weighted Shortest Path (WSP)](#weighted-shortest-path)
|
|
|
|
|
|
## Breadth First Search
|
|
|
|
[Breadth First Search](https://en.wikipedia.org/wiki/Breadth-first_search)
|
|
is a way of traversing a graph data structure. The
|
|
traversal starts from a single node (usually referred to as source node) and,
|
|
during the traversal, breadth is prioritized over depth, hence the name of the
|
|
algorithm. More precisely, when we visit some node, we can safely assume that
|
|
we have already visited all nodes that are fewer edges away from a source node.
|
|
An interesting side-effect of traversing a graph in BFS order is the fact
|
|
that, when we visit a particular node, we can easily find a path from
|
|
the source node to the newly visited node with the least number of edges.
|
|
Since in this context we disregard the edge weights, we can say that BFS is
|
|
a solution to an unweighted shortest path problem.
|
|
|
|
The algorithm itself proceeds as follows:
|
|
|
|
* Keep around a set of nodes that are equidistant from the source node.
|
|
Initially, this set contains only the source node.
|
|
* Expand to all not yet visited nodes that are a single edge away from that
|
|
set. Note that the set of those nodes is also equidistant from the source
|
|
node.
|
|
* Replace the set with a set of nodes obtained in the previous step.
|
|
* Terminate the algorithm when the set is empty.
|
|
|
|
The order of visited nodes is nicely visualized in the following animation from
|
|
Wikipedia. Note that each row contains nodes that are equidistant from the
|
|
source and thus represents one of the sets mentioned above.
|
|
|
|
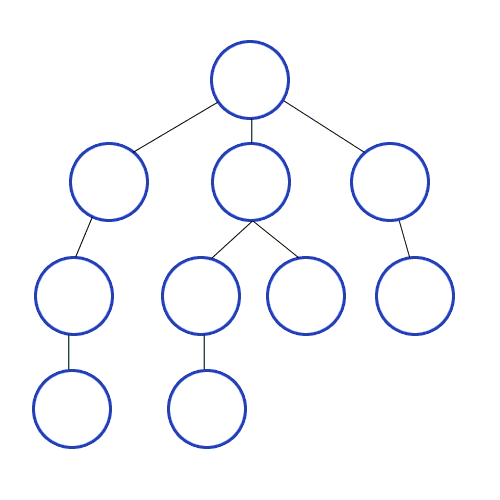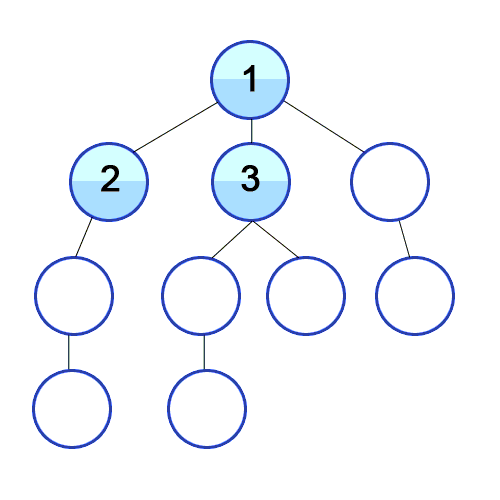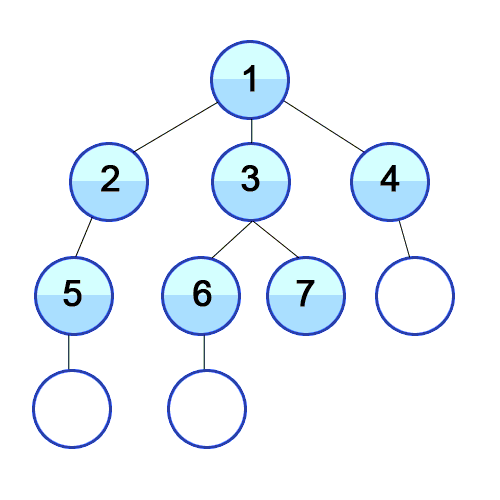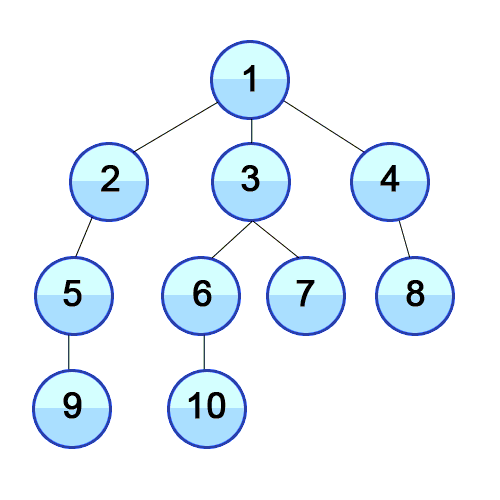
|
|
|
|
The standard BFS implementation skews from the above description by relying on
|
|
a FIFO (first in, first out) queue data structure. Nevertheless, the
|
|
functionality is equivalent and its runtime is bounded by `O(|V| + |E|)` where
|
|
`V` denotes the set of nodes and `E` denotes the set of edges. Therefore,
|
|
it provides a more efficient way of finding unweighted shortest paths than
|
|
running [Dijkstra's algorithm](concept__weighted_shortest_path.md) on a graph
|
|
with edge weights equal to `1`.
|
|
|
|
## Weighted Shortest Path
|
|
|
|
In [graph theory](https://en.wikipedia.org/wiki/Graph_theory), weighted shortest
|
|
path problem is the problem of finding a path between two nodes in a graph such
|
|
that the sum of the weights of edges connecting nodes on the path is minimized.
|
|
|
|
### Dijkstra's algorithm
|
|
|
|
One of the most important algorithms for finding weighted shortest paths is
|
|
[Dijkstra's algorithm](https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm).
|
|
Our implementation uses a modified version of this algorithm that can handle
|
|
length restriction. The length restriction parameter is optional and when it's
|
|
not set it could increase the complexity of the algorithm. It is important to
|
|
note that the term "length" in this context denotes the number of traversed
|
|
edges and not the sum of their weights.
|
|
|
|
The algorithm itself is based on a couple of greedy observations and could
|
|
be expressed in natural language as follows:
|
|
|
|
* Keep around a set of already visited nodes along with their corresponding
|
|
shortest paths from source node. Initially, this set contains only the
|
|
source node with the shortest distance of `0`.
|
|
* Find an edge that goes from a visited node to an unvisited one such that the
|
|
shortest path from source to the visited node increased by the weight of
|
|
that edge is minimized. Traverse that edge and add a newly visited node with
|
|
appropriate distance to the set of already visited nodes.
|
|
* Repeat the process until the destination node is visited.
|
|
|
|
The described algorithm is nicely visualized in the following animation from
|
|
Wikipedia. Note that edge weights correspond to the Euclidean distance between
|
|
nodes which represent points on a plane.
|
|
|
|
|
|
|
|
Using appropriate data structures the worst-case performance of our
|
|
implementation can be expressed as `O(|E| + |V|log|V|)` where `E` denotes
|
|
a set of edges and `V` denotes the set of nodes.
|
|
|
|
A sample query that finds a shortest path between two nodes looks as follows:
|
|
|
|
```opencypher
|
|
MATCH (a {id: 723})-[edge_list *wShortest 10 (e, n | e.weight) total_weight]-(b {id: 882}) RETURN *
|
|
```
|
|
|
|
This query has an upper bound length restriction set to `10`. This means that no
|
|
path that traverses more than `10` edges will be considered as a valid result.
|
|
|
|
#### Upper Bound Implications
|
|
|
|
Since the upper bound parameter is optional, we can have different results based
|
|
on this parameter.
|
|
|
|
Consider the following graph and sample queries.
|
|
|
|

|
|
|
|
```opencypher
|
|
MATCH (a {id: 0})-[edge_list *wShortest 3 (e, n | e.weight) total_weight]-(b {id: 5}) RETURN *
|
|
```
|
|
|
|
```opencypher
|
|
MATCH (a {id: 0})-[edge_list *wShortest (e, n | e.weight) total_weight]-(b {id: 5}) RETURN *
|
|
```
|
|
|
|
The first query will try to find the weighted shortest path between nodes `0`
|
|
and `5` with the restriction on the path length set to `3`, and the second query
|
|
will try to find the weighted shortest path with no restriction on the path
|
|
length.
|
|
|
|
The expected result for the first query is `0 -> 1 -> 4 -> 5` with the total
|
|
cost of `12`, while the expected result for the second query is
|
|
`0 -> 2 -> 3 -> 4 -> 5` with the total cost of `11`. Obviously, the second
|
|
query can find the true shortest path because it has no restrictions on the
|
|
length.
|
|
|
|
To handle cases when the length restriction is set, *weighted shortest path*
|
|
algorithm uses both node and distance as the state. This causes the search
|
|
space to increase by the factor of the given upper bound. On the other hand, not
|
|
setting the upper bound parameter, the search space might contain the whole
|
|
graph.
|
|
|
|
Because of this, one should always try to narrow down the upper bound limit to
|
|
be as precise as possible in order to have a more performant query.
|
|
|
|
## Where to next?
|
|
|
|
For some real-world application of WSP we encourage you to visit our article
|
|
on [exploring the European road network](tutorial__exploring_the_european_road_network.md)
|
|
which was specially crafted to showcase our graph algorithms.
|