Add graph algorithnm concepts to user_technical

Reviewers: buda

Reviewed By: buda

Differential Revision: https://phabricator.memgraph.io/D1532

docs/user_technical/concept__graph_algorithms.md

@@ -0,0 +1,156 @@
+# Graph Algorithms
+
+## Introduction
+
+The graph is a mathematical structure used to describe a set of objects in which
+some pairs of objects are "related" in some sense. Generally, we consider
+those objects as abstractions named `nodes` (also called `vertices`).
+Aforementioned relations between nodes are modelled by an abstraction named
+`edge` (also called `relationship`).
+
+It turns out that a lot of real-world problems can be successfully modeled
+using graphs. Some natural examples would contain railway networks between
+cities, computer networks, piping systems and Memgraph itself.
+
+This article outlines some of the most important graph algorithms
+that are internally used by Memgraph. We believe that advanced users could
+significantly benefit from obtaining basic knowledge about those algorithms.
+The users should also note that this article does not contain an in-depth
+analysis of algorithms and their implementation details since those are
+well documented in the appropriate literature and, in our opinion, go well out
+of scope for user documentation. That being said, we will include the relevant
+information for using Memgraph effectively and efficiently.
+
+Contents of this article include:
+
+  * [Breadth First Search (BFS)](#breadth-first-search)
+  * [Weighted Shortest Path (WSP)](#weighted-shortest-path)
+
+
+## Breadth First Search
+
+[Breadth First Search](https://en.wikipedia.org/wiki/Breadth-first_search)
+is a way of traversing a graph data structure. The
+traversal starts from a single node (usually referred to as source node) and,
+during the traversal, breadth is prioritized over depth, hence the name of the
+algorithm. More precisely, when we visit some node, we can safely assume that
+we have already visited all nodes that are fewer edges away from a source node.  
+An interesting side-effect of traversing a graph in BFS order is the fact
+that, when we visit a particular node, we can easily find a path from
+the source node to the newly visited node with the least number of edges.
+Since in this context we disregard the edge weights, we can say that BFS is
+a solution to an unweighted shortest path problem.
+
+The algorithm itself proceeds as follows:
+
+  * Keep around a set of nodes that are equidistant from the source node.
+    Initially, this set contains only the source node.
+  * Expand to all not yet visited nodes that are a single edge away from that
+    set. Note that the set of those nodes is also equidistant from the source
+    node.
+  * Replace the set with a set of nodes obtained in the previous step.
+  * Terminate the algorithm when the set is empty.
+
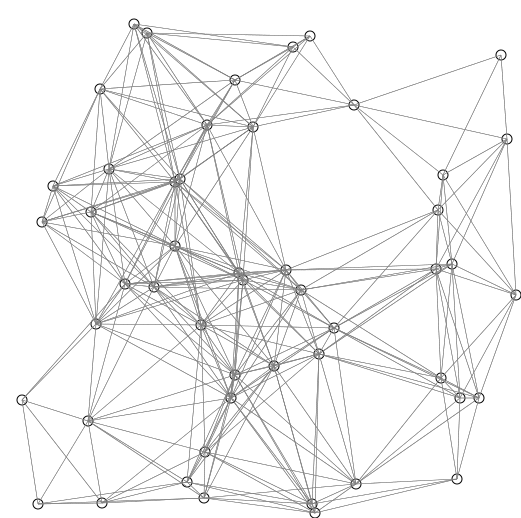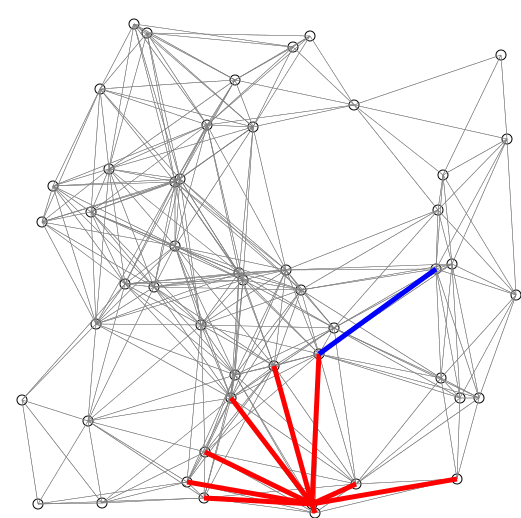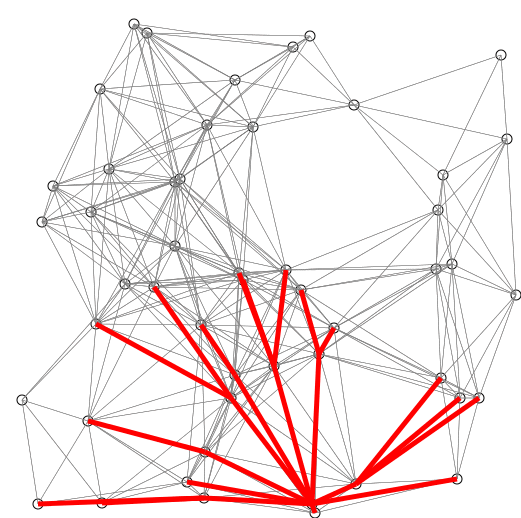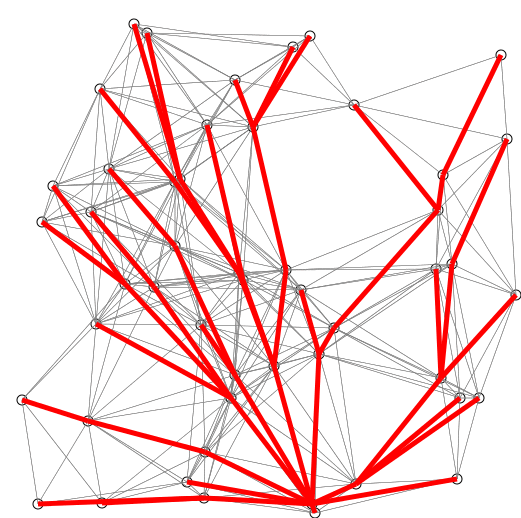
+The order of visited nodes is nicely visualized in the following animation from
+Wikipedia. Note that each row contains nodes that are equidistant from the
+source and thus represents one of the sets mentioned above.
+
+![visualization](https://upload.wikimedia.org/wikipedia/commons/5/5d/Breadth-First-Search-Algorithm.gif)
+
+The standard BFS implementation skews from the above description by relying on
+a FIFO (first in, first out) queue data structure. Nevertheless, the
+functionality is equivalent and its runtime is bounded by `O(|V| + |E|)` where
+`V` denotes the set of nodes and `E` denotes the set of edges. Therefore,
+it provides a more efficient way of finding unweighted shortest paths than
+running [Dijkstra's algorithm](concept__weighted_shortest_path.md) on a graph
+with edge weights equal to `1`.
+
+## Weighted Shortest Path
+
+In [graph theory](https://en.wikipedia.org/wiki/Graph_theory), weighted shortest
+path problem is the problem of finding a path between two nodes in a graph such
+that the sum of the weights of edges connecting nodes on the path is minimized.
+
+### Dijkstra's algorithm
+
+One of the most important algorithms for finding weighted shortest paths is
+[Dijkstra's algorithm](https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm).
+Our implementation uses a modified version of this algorithm that can handle
+length restriction. The length restriction parameter is optional and when it's
+not set it could increase the complexity of the algorithm. It is important to
+note that the term "length" in this context denotes the number of traversed
+edges and not the sum of their weights.
+
+The algorithm itself is based on a couple of greedy observations and could
+be expressed in natural language as follows:
+
+  * Keep around a set of already visited nodes along with their corresponding
+    shortest paths from source node. Initially, this set contains only the
+    source node with the shortest distance of `0`.
+  * Find an edge that goes from a visited node to an unvisited one such that the
+    shortest path from source to the visited node increased by the weight of
+    that edge is minimized. Traverse that edge and add a newly visited node with
+    appropriate distance to the set of already visited nodes.
+  * Repeat the process until the destination node is visited.
+
+The described algorithm is nicely visualized in the following animation from
+Wikipedia. Note that edge weights correspond to the Euclidean distance between
+nodes which represent points on a plane.
+
+![visualization](https://upload.wikimedia.org/wikipedia/commons/e/e4/DijkstraDemo.gif)
+
+Using appropriate data structures the worst-case performance of our
+implementation can be expressed as  `O(|E| + |V|log|V|)` where `E` denotes
+a set of edges and `V` denotes the set of nodes.
+
+A sample query that finds a shortest path between two nodes looks as follows:
+
+```opencypher
+MATCH (a {id: 723})-[edge_list *wShortest 10 (e, n | e.weight) total_weight]-(b {id: 882}) RETURN *
+```
+
+This query has an upper bound length restriction set to `10`. This means that no
+path that traverses more than `10` edges will be considered as a valid result.
+
+#### Upper Bound Implications
+
+Since the upper bound parameter is optional, we can have different results based
+on this parameter.
+
+Consider the following graph and sample queries.
+
+![sample-graph](data/graph.png)
+
+```opencypher
+MATCH (a {id: 0})-[edge_list *wShortest 3 (e, n | e.weight) total_weight]-(b {id: 5}) RETURN *
+```
+
+```opencypher
+MATCH (a {id: 0})-[edge_list *wShortest   (e, n | e.weight) total_weight]-(b {id: 5}) RETURN *
+```
+
+The first query will try to find the weighted shortest path between nodes `0`
+and `5` with the restriction on the path length set to `3`, and the second query
+will try to find the weighted shortest path with no restriction on the path
+length.
+
+The expected result for the first query is `0 -> 1 -> 4 -> 5` with the total
+cost of `12`, while the expected result for the second query is
+`0 -> 2 -> 3 -> 4 -> 5` with the total cost of `11`. Obviously, the second
+query can find the true shortest path because it has no restrictions on the
+length.
+
+To handle cases when the length restriction is set, *weighted shortest path*
+algorithm uses both node and distance as the state. This causes the search
+space to increase by the factor of the given upper bound. On the other hand, not
+setting the upper bound parameter, the search space might contain the whole
+graph.
+
+Because of this, one should always try to narrow down the upper bound limit to
+be as precise as possible in order to have a more performant query.
+
+## Where to next?
+
+For some real-world application of WSP we encourage you to visit our article
+on [exploring the European road network](tutorial__exploring_the_european_road_network.md)
+which was specially crafted to showcase our graph algorithms.