document/ddia_read
2
0
Fork 0
mirror of https://github.com/DistSysCorp/ddia.git synced 2024-12-25 20:30:39 +08:00
Code Issues Packages Projects Releases Wiki Activity
63428bab6d
ddia_read/ch03.md
harlyqiu e98862fa75 Fix typo in ch03 and ch04
2023-03-24 16:50:51 +08:00

33 KiB
Raw Blame History

DDIA 逐章精读（三）：存储和查询

第二章讲了上层抽象：数据模型和查询语言。 本章下沉一些，聚焦数据库底层如何处理查询和存储。这其中，有个逻辑链条：

使用场景 → 查询类型 → 存储格式。

查询类型主要分为两大类：

引擎类型 请求数量 数据量 瓶颈 存储格式 用户 场景举例 产品举例
OLTP 相对频繁，侧重在线交易 总体和单次查询都相对较小 Disk Seek 多用行存 比较普遍，一般应用用的比较多 银行交易 MySQL
OLAP 相对较少，侧重离线分析 总体和单次查询都相对巨大 Disk Bandwidth 列存逐渐流行 多为商业用户 商业分析 ClickHouse

其中，OLTP 侧，常用的存储引擎又有两种流派：

流派 主要特点 基本思想 代表
log-structured 流 只允许追加，所有修改都表现为文件的追加和文件整体增删 变随机写为顺序写 Bitcask、LevelDB、RocksDB、Cassandra、Lucene
update-in-place 流 以页（page）为粒度对磁盘数据进行修改 面向页、查找树 B 族树，所有主流关系型数据库和一些非关系型数据库

此外，针对 OLTP，还探索了常见的建索引的方法，以及一种特殊的数据库——全内存数据库。

对于数据仓库，本章分析了它与 OLTP 的主要不同之处。数据仓库主要侧重于聚合查询，需要扫描很大量的数据，此时，索引就相对不太有用。需要考虑的是存储成本、带宽优化等，由此引出列式存储。

驱动数据库的底层数据结构

本节由一个 shell 脚本出发，到一个相当简单但可用的存储引擎 Bitcask，然后引出 LSM-tree，他们都属于日志流范畴。之后转向存储引擎另一流派——B 族树，之后对其做了简单对比。最后探讨了存储中离不开的结构——索引。

首先来看，世界上“最简单”的数据库，由两个 Bash 函数构成：

#!/bin/bash
db_set () {
	echo "$1,$2" >> database
}

db_get () {
	grep "^$1," database | sed -e "s/^$1,//" | tail -n 1
}

这两个函数实现了一个基于字符串的 KV 存储（只支持 get/set，不支持 delete）：

$ db_set 123456 '{"name":"London","attractions":["Big Ben","London Eye"]}'
$ db_set 42 '{"name":"San Francisco","attractions":["Golden Gate Bridge"]}'
$ db_get 42
{"name":"San Francisco","attractions":["Golden Gate Bridge"]}

来分析下它为什么 work，也反映了日志结构存储的最基本原理：

  1. set：在文件末尾追加一个 KV 对。
  2. get：匹配所有 Key，返回最后（也即最新）一条 KV 对中的 Value。

可以看出：写很快，但是读需要全文逐行扫描，会慢很多。典型的以读换写。为了加快读，我们需要构建索引：一种允许基于某些字段查找的额外数据结构。

索引从原数据中构建，只为加快查找。因此索引会耗费一定额外空间，和插入时间（每次插入要更新索引），即，重新以空间和写换读取。

这便是数据库存储引擎设计和选择时最常见的权衡（trade off）：

  1. 恰当的存储格式能加快写（日志结构），但是会让读取很慢；也可以加快读（查找树、B 族树），但会让写入较慢。
  2. 为了弥补读性能，可以构建索引。但是会牺牲写入性能和耗费额外空间。

存储格式一般不好动，但是索引构建与否，一般交予用户选择。

哈希索引

本节主要基于最基础的 KV 索引。

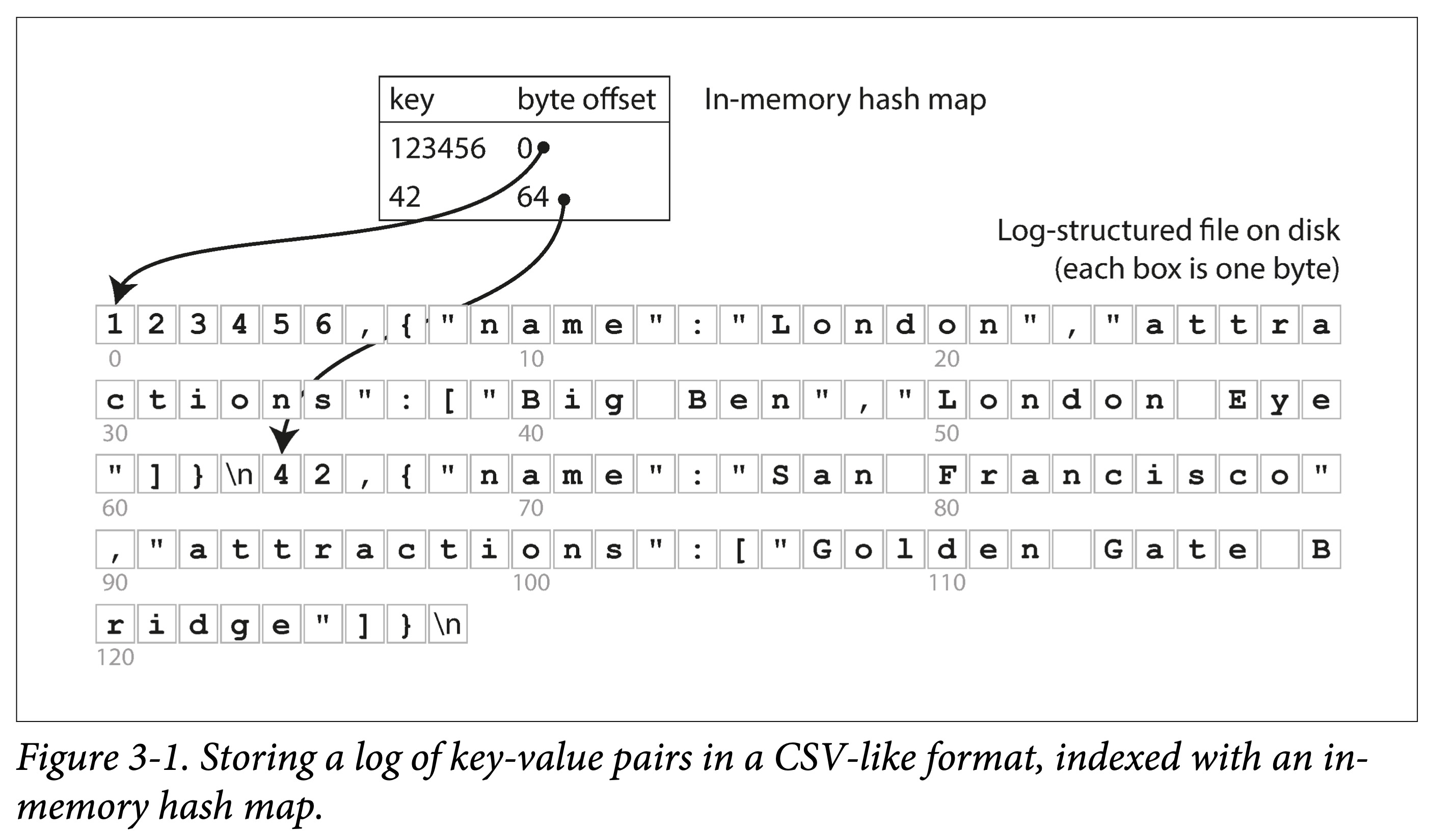
依上小节的例子，所有数据顺序追加到磁盘上。为了加快查询，我们在内存中构建一个哈希索引：

  1. Key 是查询 Key
  2. Value 是 KV 条目的起始位置和长度。

ddia-3-1-hash-map-csv.png

看来很简单，但这正是 Bitcask 的基本设计，但关键是，他 Work（在小数据量时，即所有 key 都能存到内存中时）：能提供很高的读写性能：

  1. 写：文件追加写。
  2. 读：一次内存查询，一次磁盘 seek；如果数据已经被缓存，则 seek 也可以省掉。

如果你的 key 集合很小（意味着能全放内存），但是每个 key 更新很频繁，那么 Bitcask 便是你的菜。举个栗子：频繁更新的视频播放量，key 是视频 url，value 是视频播放量。

但有个很重要问题，单个文件越来越大，磁盘空间不够怎么办？

在文件到达一定尺寸后，就新建一个文件，将原文件变为只读。同时为了回收多个 key 多次写入的造成的空间浪费，可以将只读文件进行紧缩（compact），将旧文件进行重写，挤出“水分”（被覆写的数据）以进行垃圾回收。

ddia-3-3-compaction-sim.png

当然，如果我们想让其工业可用，还有很多问题需要解决：

  1. 文件格式。对于日志来说，CSV 不是一种紧凑的数据格式，有很多空间浪费。比如，可以用 length + record bytes。
  2. 记录删除。之前只支持 put\get，但实际还需要支持 delete。但日志结构又不支持更新，怎么办呢？一般是写一个特殊标记（比如墓碑记录，tombstone）以表示该记录已删除。之后 compact 时真正删除即可。
  3. 宕机恢复。在机器重启时，内存中的哈希索引将会丢失。当然，可以全盘扫描以重建，但通常一个小优化是，对于每个 segment file，将其索引条目和数据文件一块持久化，重启时只需加载索引条目即可。
  4. 记录写坏、少写。系统任何时候都有可能宕机，由此会造成记录写坏、少写。为了识别错误记录，我们需要增加一些校验字段，以识别并跳过这种数据。为了跳过写了部分的数据，还要用一些特殊字符来标识记录间的边界。
  5. 并发控制。由于只有一个活动（追加）文件，因此写只有一个天然并发度。但其他的文件都是不可变的（compact 时会读取然后生成新的），因此读取和紧缩可以并发执行。

乍一看，基于日志的存储结构存在折不少浪费：需要以追加进行更新和删除。但日志结构有几个原地更新结构无法做的优点：

  1. 以顺序写代替随机写。对于磁盘和 SSD，顺序写都要比随机写快几个数量级。
  2. 简易的并发控制。由于大部分的文件都是不可变（immutable） 的，因此更容易做并发读取和紧缩。也不用担心原地更新会造成新老数据交替。
  3. 更少的内部碎片。每次紧缩会将垃圾完全挤出。但是原地更新就会在 page 中留下一些不可用空间。

当然，基于内存的哈希索引也有其局限：

  1. 所有 Key 必须放内存。一旦 Key 的数据量超过内存大小，这种方案便不再 work。当然你可以设计基于磁盘的哈希表，但那又会带来大量的随机写。
  2. 不支持范围查询。由于 key 是无序的，要进行范围查询必须全表扫描。

后面讲的 LSM-Tree 和 B+ 树，都能部分规避上述问题。

  • 想想，会如何进行规避？

SSTables 和 LSM-Trees

这一节层层递进，步步做引，从 SSTables 格式出发，牵出 LSM-Trees 全貌。

对于 KV 数据，前面的 BitCask 存储结构是：

  1. 外存上日志片段
  2. 内存中的哈希表

其中外存上的数据是简单追加写而形成的，并没有按照某个字段有序。

假设加一个限制，让这些文件按 key 有序。我们称这种格式为：SSTable（Sorted String Table）。

这种文件格式有什么优点呢？

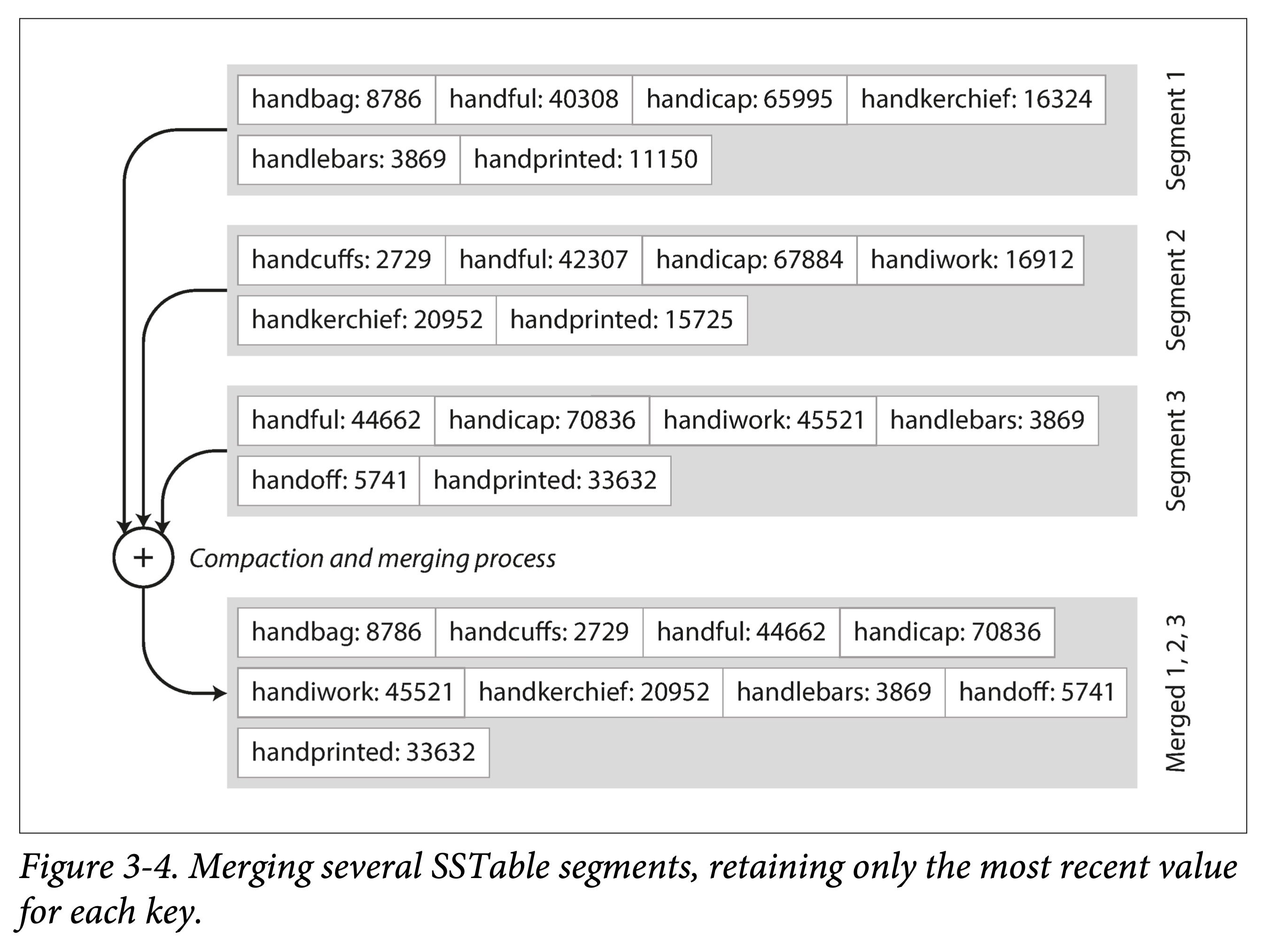
高效的数据文件合并。即有序文件的归并外排，顺序读，顺序写。不同文件出现相同 Key 怎么办？

ddia-3-4-merge-sst.png

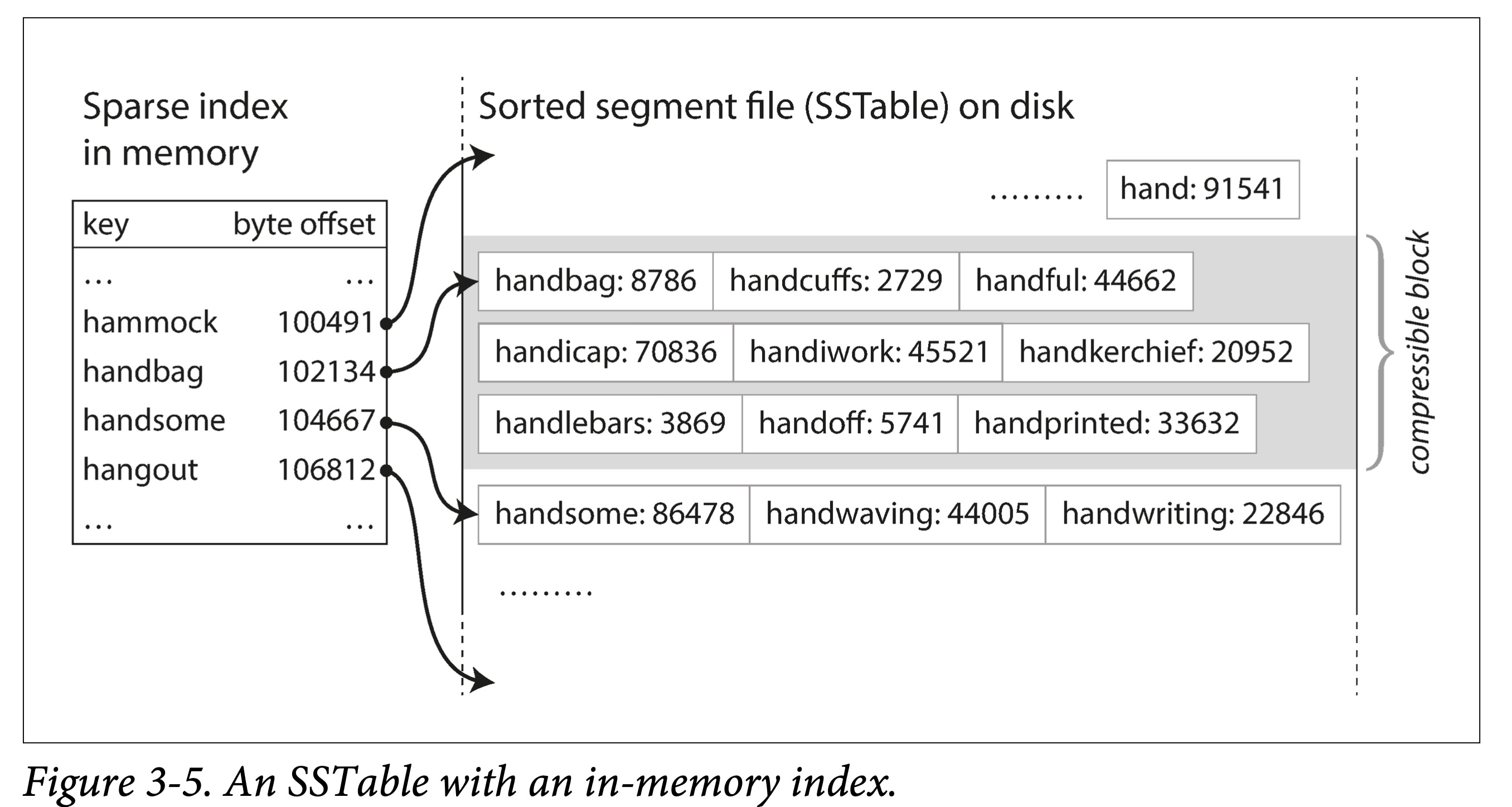
不需要在内存中保存所有数据的索引。仅需要记录下每个文件界限（以区间表示：[startKey, endKey]，当然实际会记录的更细）即可。查找某个 Key 时，去所有包含该 Key 的区间对应的文件二分查找即可。

ddia-3-5-sst-index.png

分块压缩，节省空间，减少 IO。相邻 Key 共享前缀，既然每次都要批量取，那正好一组 key batch 到一块，称为 block，且只记录 block 的索引。

构建和维护 SSTables

SSTables 格式听起来很美好，但须知数据是乱序的来的，我们如何得到有序的数据文件呢？

这可以拆解为两个小问题：

  1. 如何构建。
  2. 如何维护。

构建 SSTable 文件。将乱序数据在外存（磁盘 or SSD）中上整理为有序文件，是比较难的。但是在内存就方便的多。于是一个大胆的想法就形成了：

  1. 在内存中维护一个有序结构（称为 MemTable）。红黑树、AVL 树、跳表。
  2. 到达一定阈值之后全量 dump 到外存。

维护 SSTable 文件。为什么需要维护呢？首先要问，对于上述复合结构，我们怎么进行查询：

  1. 先去 MemTable 中查找，如果命中则返回。
  2. 再去 SSTable 按时间顺序由新到旧逐一查找。

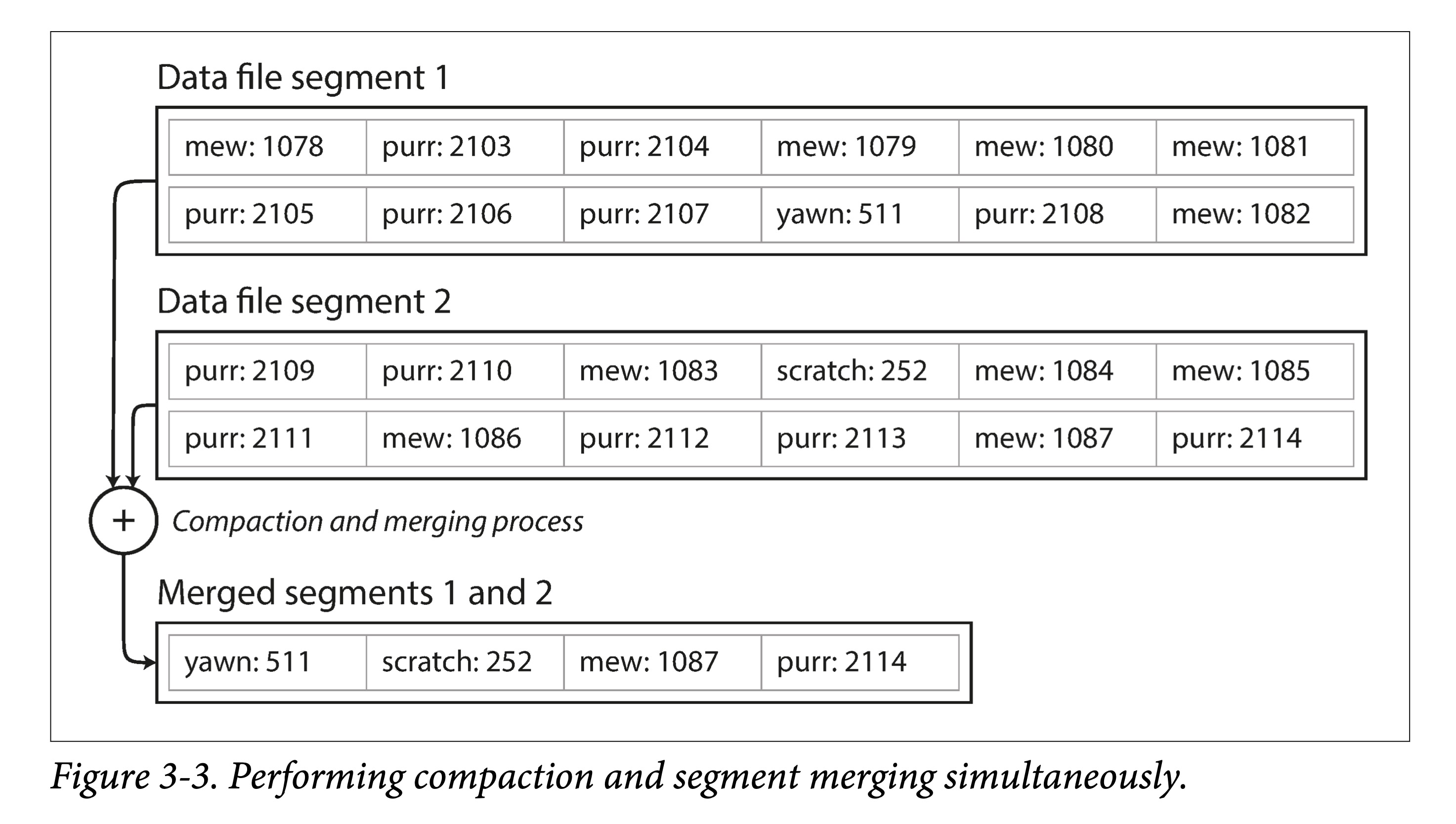
如果 SSTable 文件越来越多，则查找代价会越来越大。因此需要将多个 SSTable 文件合并，以减少文件数量，同时进行 GC，我们称之为紧缩（ Compaction）。

该方案的问题：如果出现宕机，内存中的数据结构将会消失。解决方法也很经典：WAL。

从 SSTables 到 LSM-Tree

将前面几节的一些碎片有机的组织起来，便是时下流行的存储引擎 LevelDB 和 RocksDB 后面的存储结构：LSM-Tree：

ddia-3-leveldb-architecture.png

这种数据结构是 Patrick O’Neil 等人，在 1996 年提出的：The Log-Structured Merge-Tree。

Elasticsearch 和 Solr 的索引引擎 Lucene，也使用类似 LSM-Tree 存储结构。但其数据模型不是 KV，但类似：word → document list。

性能优化

如果想让一个引擎工程上可用，还会做大量的性能优化。对于 LSM-Tree 来说，包括：

优化 SSTable 的查找。常用 Bloom Filter。该数据结构可以使用较少的内存为每个 SSTable 做一些指纹，起到一些初筛的作用。

层级化组织 SSTable。以控制 Compaction 的顺序和时间。常见的有 size-tiered 和 leveled compaction。LevelDB 便是支持后者而得名。前者比较简单粗暴，后者性能更好，也因此更为常见。

ddia-sized-tierd-compact.png

对于 RocksDB 来说，工程上的优化和使用上的优化就更多了。在其 Wiki 上随便摘录几点：

  1. Column Family
  2. 前缀压缩和过滤
  3. 键值分离，BlobDB

但无论有多少变种和优化，LSM-Tree 的核心思想——保存一组合理组织、后台合并的 SSTables ——简约而强大。可以方便的进行范围遍历，可以变大量随机为少量顺序。

B 族树

虽然先讲的 LSM-Tree，但是它要比 B+ 树新的多。

B 树于 1970 年被 R. Bayer and E. McCreight 提出后，便迅速流行了起来。现在几乎所有的关系型数据中，它都是数据索引标准一般的实现。

与 LSM-Tree 一样，它也支持高效的点查和范围查。但却使用了完全不同的组织方式。

其特点有：

  1. 以页（在磁盘上叫 page，在内存中叫 block，通常为 4k）为单位进行组织。
  2. 页之间以页 ID 来进行逻辑引用，从而组织成一颗磁盘上的树。

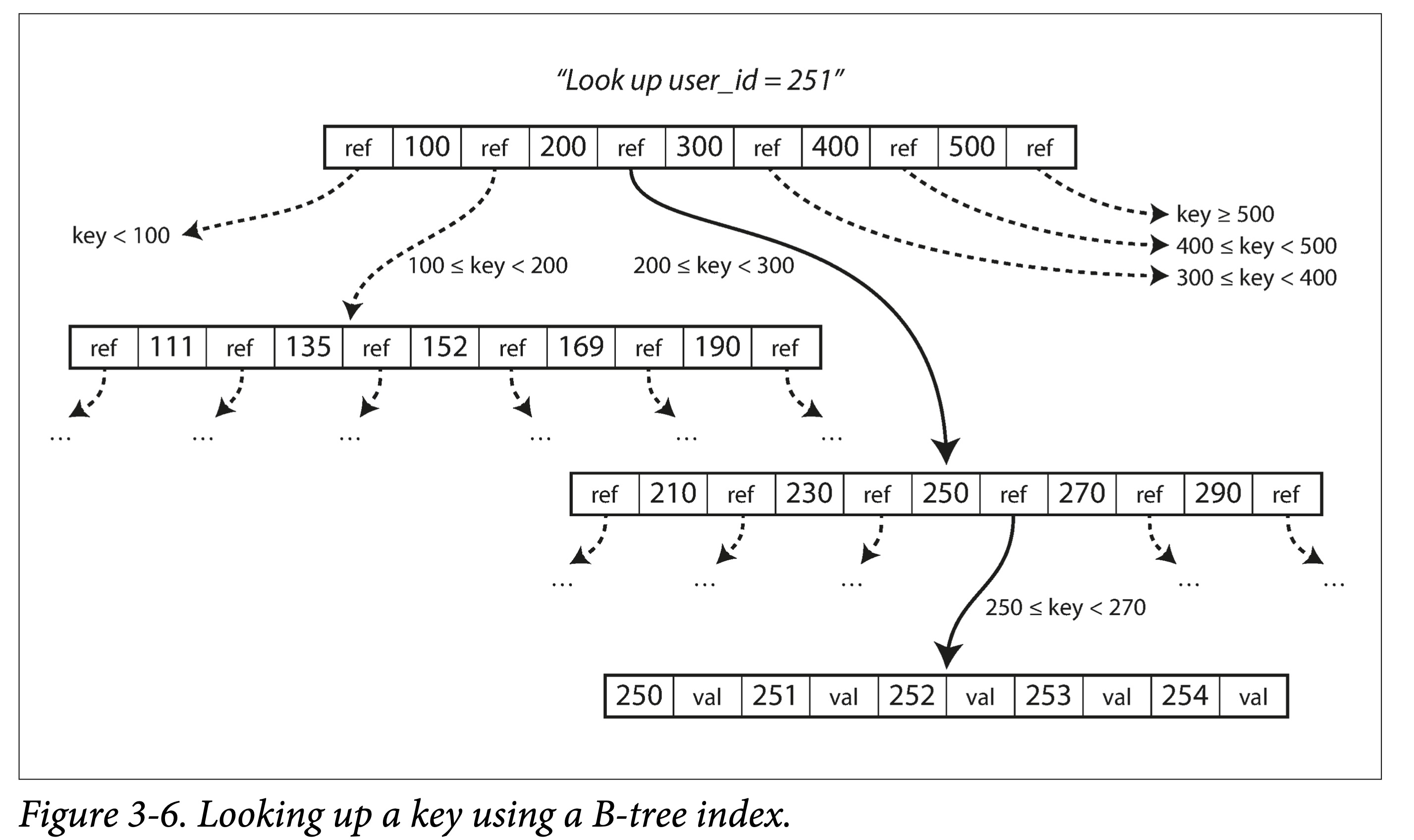
ddia-3-6-b-tree-lookup.png

查找。从根节点出发，进行二分查找，然后加载新的页到内存中，继续二分，直到命中或者到叶子节点。查找复杂度，树的高度—— O(lgn)，影响树高度的因素：分支因子（分叉数，通常是几百个）。

ddia-3-7-b-tree-grow-by-split.png

插入 or 更新。和查找过程一样，定位到原 Key 所在页，插入或者更新后，将页完整写回。如果页剩余空间不够，则分裂后写入。

分裂 or 合并。级联分裂和合并。

  • 一个记录大于一个 page 怎么办？ 树的节点是逻辑概念，page or block 是物理概念。一个逻辑节点可以对应多个物理 page。

让 B 树更可靠

B 树不像 LSM-Tree，会在原地修改数据文件。

在树结构调整时，可能会级联修改很多 Page。比如叶子节点分裂后，就需要写入两个新的叶子节点，和一个父节点（更新叶子指针）。

  1. 增加预写日志（WAL），将所有修改操作记录下来，预防宕机时中断树结构调整而产生的混乱现场。
  2. 使用 latch 对树结构进行并发控制。

B 树的优化

B 树出来了这么久，因此有很多优化：

  1. 不使用 WAL，而在写入时利用 Copy On Write 技术。同时，也方便了并发控制。如 LMDB、BoltDB。
  2. 对中间节点的 Key 做压缩，保留足够的路由信息即可。以此，可以节省空间，增大分支因子。
  3. 为了优化范围查询，有的 B 族树将叶子节点存储时物理连续。但当数据不断插入时，维护此有序性的代价非常大。
  4. 为叶子节点增加兄弟指针，以避免顺序遍历时的回溯。即 B+ 树的做法，但远不局限于 B+ 树。
  5. B 树的变种，分形树，从 LSM-tree 借鉴了一些思想以优化 seek。

B-Trees 和 LSM-Trees 对比

存储引擎 B-Tree LSM-Tree 备注
优势 读取更快 写入更快
写放大 1. 数据和 WAL
2. 更改数据时多次覆盖整个 Page		 1. 数据和 WAL
2. Compaction		 SSD 不能过多擦除。因此 SSD 内部的固件中也多用日志结构来减少随机小写。
写吞吐 相对较低：
1. 大量随机写。		 相对较高：
1. 较低的写放大（取决于数据和配置）
2. 顺序写入。
3. 更为紧凑。
压缩率 1. 存在较多内部碎片。 1. 更加紧凑，没有内部碎片。
2. 压缩潜力更大（共享前缀）。		 但紧缩不及时会造成 LSM-Tree 存在很多垃圾
后台流量 1. 更稳定可预测，不会受后台 compaction 突发流量影响。 1. 写吞吐过高，compaction 跟不上，会进一步加重读放大。
2. 由于外存总带宽有限，compaction 会影响读写吞吐。
3. 随着数据越来越多，compaction 对正常写影响越来越大。		 RocksDB 写入太过快会引起 write stall，即限制写入，以期尽快 compaction 将数据下沉。
存储放大 1. 有些 Page 没有用满 1. 同一个 Key 存多遍
并发控制 1. 同一个 Key 只存在一个地方
2. 树结构容易加范围锁。		 同一个 Key 会存多遍，一般使用 MVCC 进行控制。

其他索引结构

次级索引（secondary indexes）。即，非主键的其他属性到该元素（SQL 中的行，MongoDB 中的文档和图数据库中的点和边）的映射。

聚集索引和非聚集索引（cluster indexes and non-cluster indexes）

对于存储数据和组织索引，我们可以有多种选择：

  1. 数据本身无序的存在文件中，称为 堆文件（heap file），索引的值指向对应数据在 heap file 中的位置。这样可以避免多个索引时的数据拷贝。
  2. 数据本身按某个字段有序存储，该字段通常是主键。则称基于此字段的索引为聚集索引（clustered index），从另外一个角度理解，即将索引和数据存在一块。则基于其他字段的索引为非聚集索引，在索引中仅存数据的引用。
  3. 一部分列内嵌到索引中存储，一部分列数据额外存储。称为覆盖索引（covering index）   或  包含列的索引（index with included columns）。

索引可以加快查询速度，但需要占用额外空间，并且牺牲了部分更新开销，且需要维持某种一致性。

多列索引（Multi-column indexes）。

现实生活中，多个字段联合查询更为常见。比如查询某个用户周边一定范围内的商户，需要经度和纬度二维查询。

SELECT * FROM restaurants WHERE latitude > 51.4946 AND latitude < 51.5079
                            AND longitude > -0.1162 AND longitude < -0.1004;

可以：

  1. 将二维编码为一维，然后按普通索引存储。
  2. 使用特殊数据结构，如 R 树。

全文索引和模糊索引（Full-text search and fuzzy indexes）。

前述索引只提供全字段的精确匹配，而不提供类似搜索引擎的功能。比如，按字符串中包含的单词查询，针对笔误的单词查询。

在工程中常用 Apace Lucene 库，和其包装出来的服务：Elasticsearch。他也使用类似 LSM-tree 的日志存储结构，但其索引是一个有限状态自动机，在行为上类似 Trie 树。

全内存数据结构

随着单位内存成本下降，甚至支持持久化（non-volatile memory，NVM，如 Intel 的 傲腾），全内存数据库也逐渐开始流行。

根据是否需要持久化，内存数据大概可以分为两类：

  1. 不需要持久化。如只用于缓存的 Memcached。
  2. 需要持久化。通过 WAL、定期 snapshot、远程备份等等来对数据进行持久化。但使用内存处理全部读写，因此仍是内存数据库。

VoltDB, MemSQL, and Oracle TimesTen 是提供关系模型的内存数据库。RAMCloud 是提供持久化保证的 KV 数据库。Redis and Couchbase 仅提供弱持久化保证。

内存数据库存在优势的原因不仅在于不需要读取磁盘，而在更于不需要对数据结构进行序列化、编码后以适应磁盘所带来的额外开销。

当然，内存数据库还有以下优点：

  1. 提供更丰富的数据抽象。如 set 和 queue 这种只存在于内存中的数据抽象。
  2. 实现相对简单。因为所有数据都在内存中。

此外，内存数据库还可以通过类似操作系统 swap 的方式，提供比物理机内存更大的存储空间，但由于其有更多数据库相关信息，可以将换入换出的粒度做的更细、性能做的更好。

基于非易失性存储器（non-volatile memory，NVM）的存储引擎也是这些年研究的一个热点。

事务型还是分析型

术语 OL（Online）主要是指交互式的查询。

术语事务（transaction）由来有一些历史原因。早期的数据库使用方多为商业交易（commercial），比如买卖、发工资等等。但是随着数据库应用不断扩大，交易\事务作为名词保留了下来。

事务不一定具有 ACID 特性，事务型处理多是随机的以较低的延迟进行读写，与之相反，分析型处理多为定期的批处理，延迟较高。

下表是一个对比：

属性 OLTP OLAP
主要读取模式 小数据量的随机读，通过 key 查询 大数据量的聚合（max,min,sum, avg）查询
主要写入模式 随机访问，低延迟写入 批量导入（ETL）或者流式写入
主要应用场景 通过 web 方式使用的最终用户 互联网分析，为了辅助决策
如何看待数据 当前时间点的最新状态 随着时间推移的
数据尺寸 通常 GB 到 TB 通常 TB 到 PB

一开始对于 AP 场景，仍然使用的传统数据库。在模型层面来说，SQL 足够灵活，能够基本满足 AP 查询需求。但在实现层面，传统数据库在 AP 负载中的表现（大数据量吞吐较低）不尽如人意，因此大家开始转向在专门设计的数据库中进行 AP 查询，我们称之为数据仓库（Data Warehouse）。

数据仓库

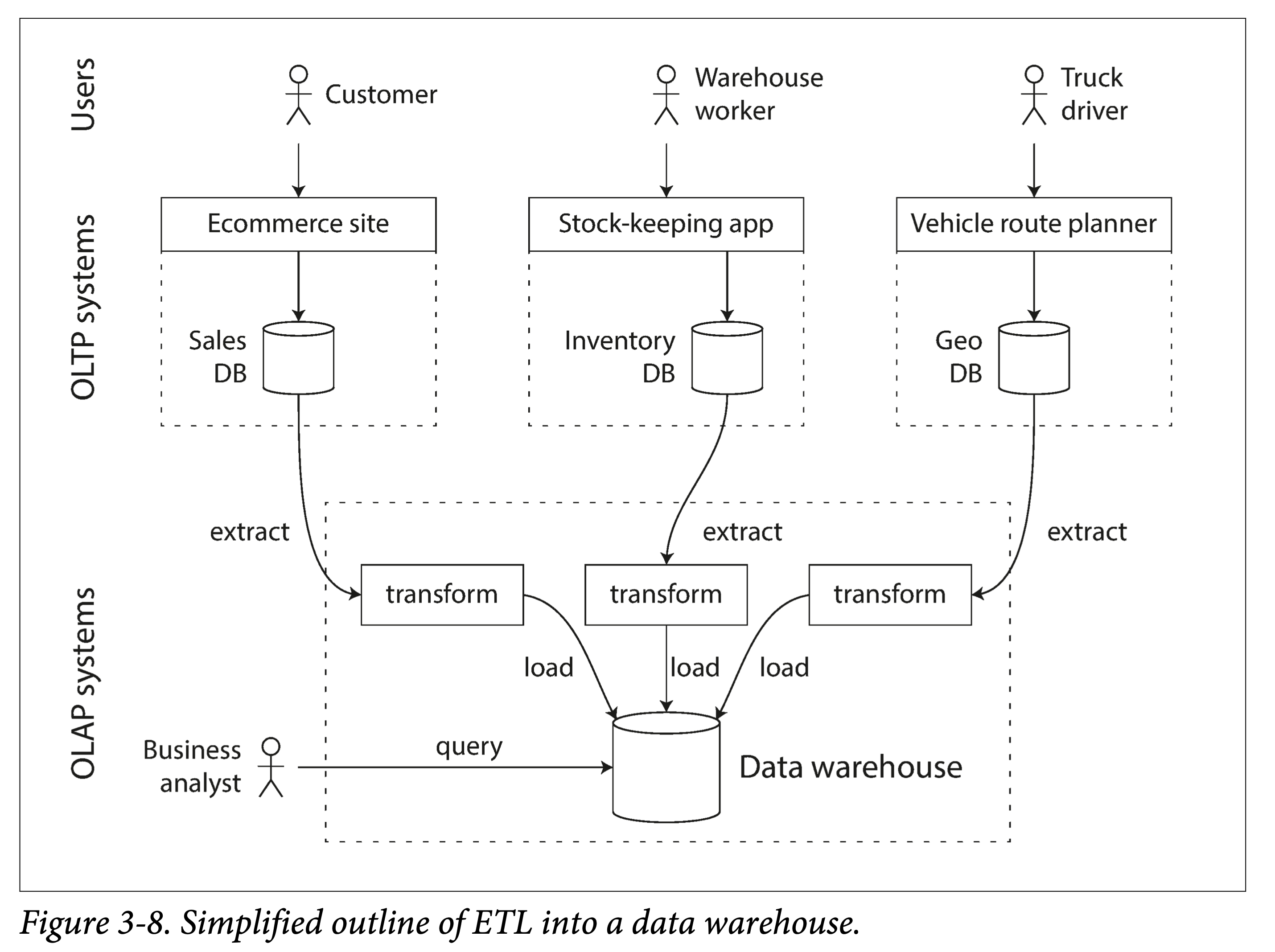
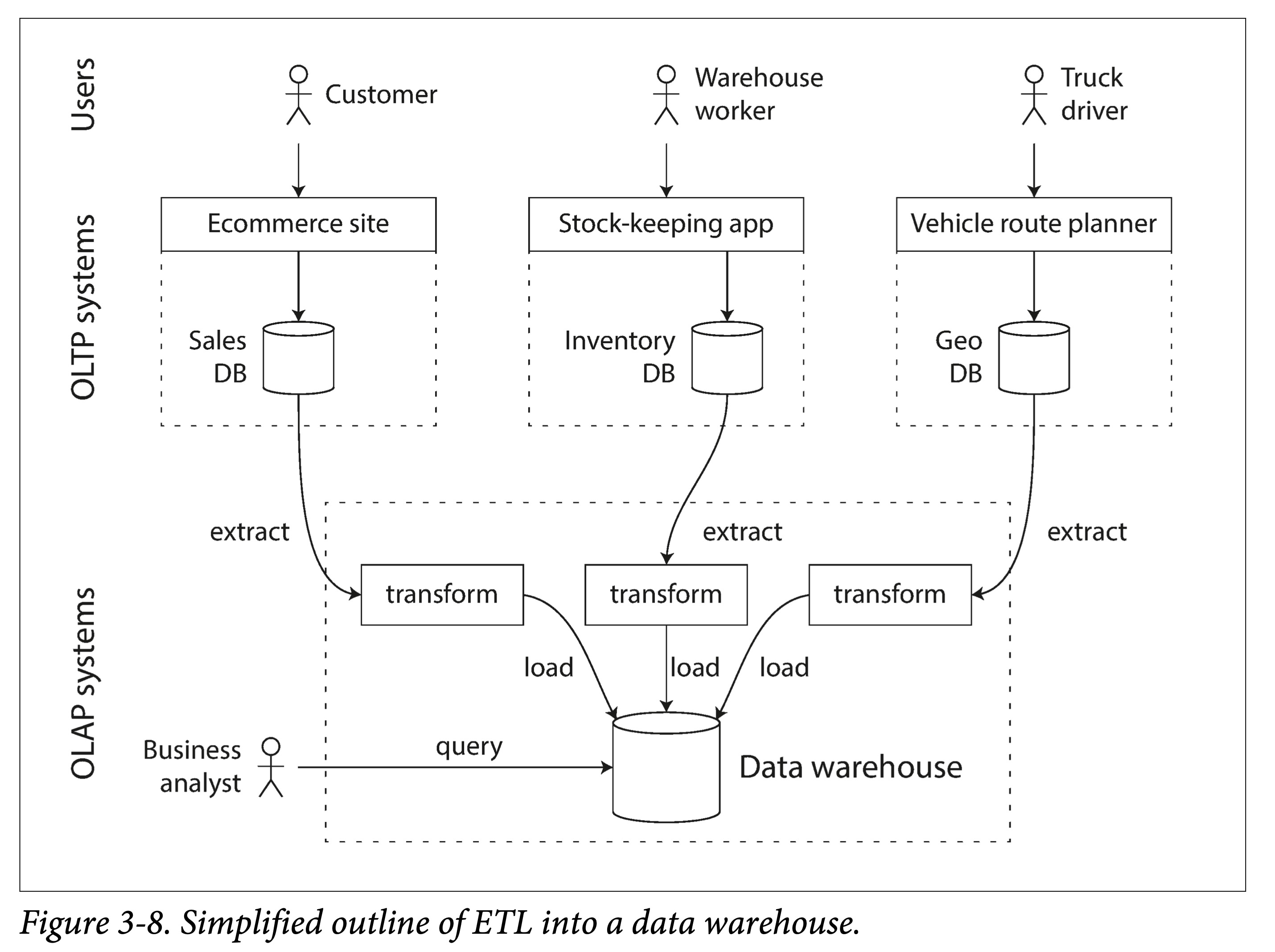
对于一个企业来说，一般都会有很多偏交易型的系统，如用户网站、收银系统、仓库管理、供应链管理、员工管理等等。通常要求高可用与低延迟，因此直接在原库进行业务分析，会极大影响正常负载。因此需要一种手段将数据从原库导入到专门的数仓。

我们称之为 ETL：extract-transform-load。

ddia-3-8-etl.png

一般企业的数据量达到一定的量级才会需要进行 AP 分析，毕竟在小数据量尺度下，用 Excel 进行聚合查询都够了。当然，现在一个趋势是，随着移动互联网、物联网的普及，接入终端的类型和数量越来越多，产生的数据增量也越来越大，哪怕初创不久的公司可能也会积存大量数据，进而也需要 AP 支持。

AP 场景下的聚合查询分析和传统 TP 型有所不同。因此，需要构建索引的方式也多有不同。

同样接口后的不同

TP 和 AP 都可以使用 SQL 模型进行查询分析。但是由于其负载类型完全不同，在查询引擎实现和存储格式优化时，做出的设计决策也就大相径庭。因此，在同一套 SQL 接口的表面下，两者对应的数据库实现结构差别很大。

虽然有的数据库系统号称两者都支持，比如之前的 Microsoft SQL Server 和 SAP HANA，但是也正日益发展成两种独立的查询引擎。近年来提的较多的 HTAP 系统也是类似，其为了 serve 不同类型负载底层其实有两套不同的存储，只不过系统内部会自动的做数据的冗余和重新组织，对用户透明。

AP 建模：星状型和雪花型

AP 中的处理模型相对较少，比较常用的有星状模型，也称为维度模型。

ddia3-9-star-schema.png

如上图所示，星状模型通常包含一张事件表（fact table） 和多张维度表（*dimension tables***）**。事件表以事件流的方式将数据组织起来，然后通过外键指向不同的维度。

星状模型的一个变种是雪花模型，可以类比雪花（❄️）图案，其特点是在维度表中会进一步进行二次细分，讲一个维度分解为几个子维度。比如品牌和产品类别可能有单独的表格。星状模型更简单，雪花模型更精细，具体应用中会做不同取舍。

在典型的数仓中，事件表可能会非常宽，即有很多的列：一百到数百列。

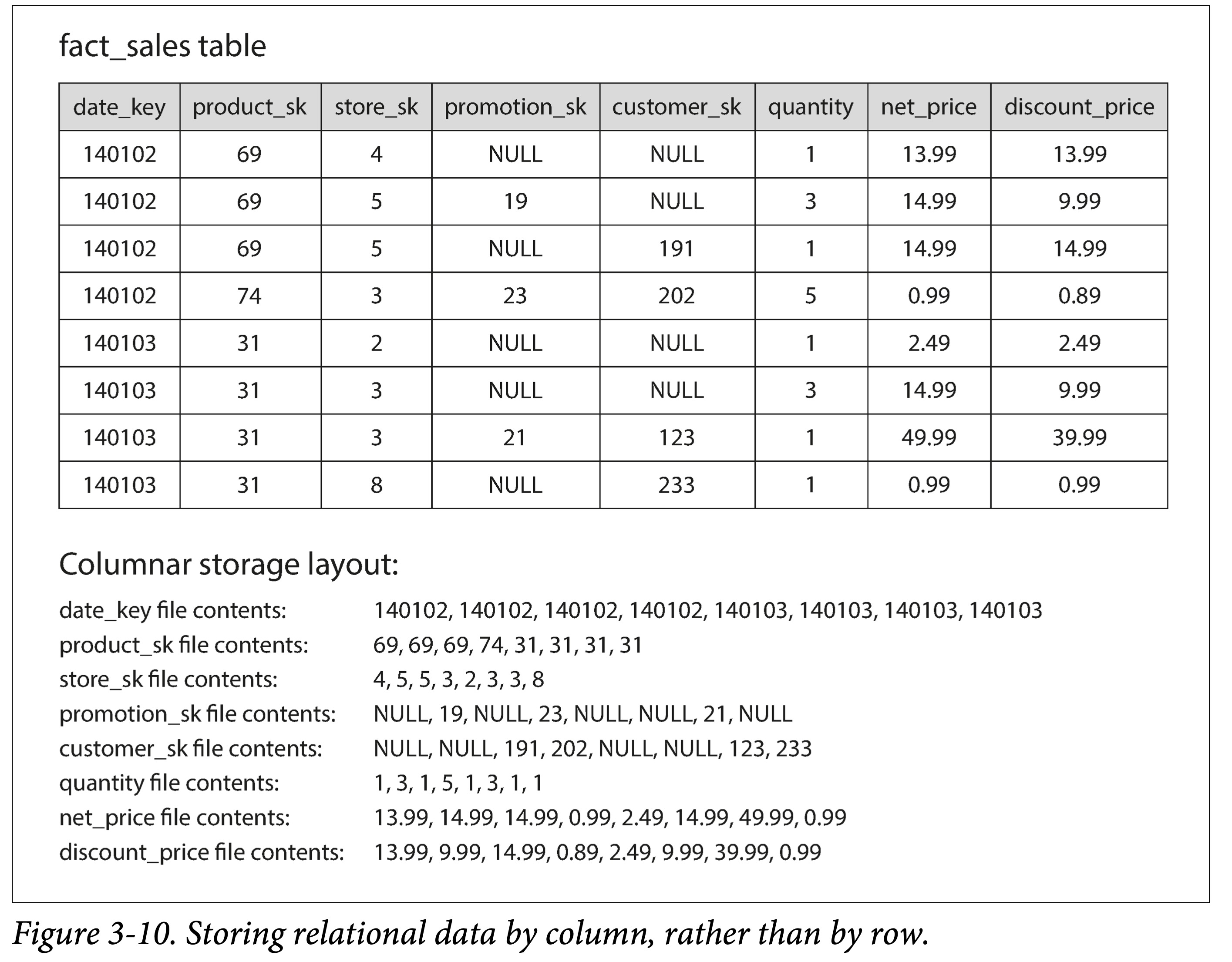
列存

前一小节提到的分维度表和事实表，对于后者来说，有可能达到数十亿行和数 PB 大。虽然事实表可能通常有几十上百列，但是单次查询通常只关注其中几个维度（列）。

如查询人们是否更倾向于在一周的某一天购买新鲜水果或糖果：

SELECT
  dim_date.weekday,
  dim_product.category,
  SUM(fact_sales.quantity) AS quantity_sold
FROM fact_sales
  JOIN dim_date ON fact_sales.date_key = dim_date.date_key
  JOIN dim_product ON fact_sales.product_sk = dim_product.product_sk
WHERE
  dim_date.year = 2013 AND
  dim_product.category IN ('Fresh fruit', 'Candy')
GROUP BY
  dim_date.weekday, dim_product.category;

由于传统数据库通常是按行存储的，这意味着对于属性（列）很多的表，哪怕只查询一个属性，也必须从磁盘上取出很多属性，无疑浪费了 IO 带宽、增大了读放大。

于是一个很自然的想法呼之欲出：每一个列分开存储好不好？

ddia-3-10-store-by-column.png

不同列之间同一个行的字段可以通过下标来对应。当然也可以内嵌主键来对应，但那样存储成本就太高了。

列压缩

将所有数据分列存储在一块，带来了一个意外的好处，由于同一属性的数据相似度高，因此更易压缩。

如果每一列中值阈相比行数要小的多，可以用位图编码（bitmap encoding）。举个例子，零售商可能有数十亿的销售交易，但只有 100,000 个不同的产品。

ddia-3-11-compress.png

上图中，是一个列分片中的数据，可以看出只有 {29, 30, 31, 68, 69, 74} 六个离散值。针对每个值出现的位置，我们使用一个 bit array 来表示：

  1. bit map 下标对应列的下标
  2. 值为 0 则表示该下标没有出现该值
  3. 值为 1 则表示该下标出现了该值

如果 bit array 是稀疏的，即大量的都是 0，只要少量的 1。其实还可以使用 游程编码（RLE，Run-length encoding） 进一步压缩：

  1. 将连续的 0 和 1，改写成 数量+值，比如 product_sk = 29 是 9 个 0，1 个 1，8 个 0。
  2. 使用一个小技巧，将信息进一步压缩。比如将同值项合并后，肯定是 0 1 交错出现，固定第一个值为 0，则交错出现的 0 和 1 的值也不用写了。则 product_sk = 29 编码变成 9，1，8
  3. 由于我们知道 bit array 长度，则最后一个数字也可以省掉，因为它可以通过 array len - sum(other lens) 得到，则 product_sk = 29 的编码最后变成：9，1

位图索引很适合应对查询中的逻辑运算条件，比如：

WHERE product_sk IN（30，68，69）

可以转换为 product_sk = 30、product_sk = 68和  product_sk = 69这三个 bit array 按位或（OR）。

WHERE product_sk = 31 AND store_sk = 3

可以转换为 product_sk = 31和  store_sk = 3的 bit array 的按位与，就可以得到所有需要的位置。

列族

书中特别提到列族（column families）。它是 Cassandra 和 HBase 中的的概念，他们都起源于自谷歌的 BigTable 。注意到他们和列式（column-oriented）存储有相似之处，但绝不完全相同：

  1. 同一个列族中多个列是一块存储的，并且内嵌行键（row key）。
  2. 并且列不压缩（存疑？）

因此 BigTable 在用的时候主要还是面向行的，可以理解为每一个列族都是一个子表。

内存带宽和向量化处理

数仓的超大规模数据量带来了以下瓶颈：

  1. 内存处理带宽
  2. CPU 分支预测错误和流水线停顿

关于内存的瓶颈可已通过前述的数据压缩来缓解。对于 CPU 的瓶颈可以使用：

  1. 列式存储和压缩可以让数据尽可能多地缓存在 L1 中，结合位图存储进行快速处理。
  2. 使用 SIMD 用更少的时钟周期处理更多的数据。

列式存储的排序

由于数仓查询多集中于聚合算子（比如 sum，avg，min，max），列式存储中的存储顺序相对不重要。但也免不了需要对某些列利用条件进行筛选，为此我们可以如 LSM-Tree 一样，对所有行按某一列进行排序后存储。

注意，不可能同时对多列进行排序。因为我们需要维护多列间的下标间的对应关系，才可能按行取数据。

同时，排序后的那一列，压缩效果会更好。

不同副本，不同排序

在分布式数据库（数仓这么大，通常是分布式的）中，同一份数据我们会存储多份。对于每一份数据，我们可以按不同列有序存储。这样，针对不同的查询需求，便可以路由到不同的副本上做处理。当然，这样也最多只能建立副本数（通常是 3 个左右）列索引。

这一想法由 C-Store 引入，并且为商业数据仓库 Vertica 采用。

列式存储的写入

上述针对数仓的优化（列式存储、数据压缩和按列排序）都是为了解决数仓中常见的读写负载，读多写少，且读取都是超大规模的数据。

我们针对读做了优化，就让写入变得相对困难。

比如 B 树的原地更新流是不太行的。举个例子，要在中间某行插入一个数据，纵向来说，会影响所有的列文件（如果不做 segment 的话）；为了保证多列间按下标对应，横向来说，又得更新该行不同列的所有列文件。

所幸我们有 LSM-Tree 的追加流。

  1. 将新写入的数据在内存中 Batch 好，按行按列，选什么数据结构可以看需求。
  2. 然后达到一定阈值后，批量刷到外存，并与老数据合并。

数仓 Vertica 就是这么做的。

聚合：数据立方和物化视图

不一定所有的数仓都是列式存储，但列式存储的种种好处让其变得流行了起来。

其中一个值得一提的是物化聚合（materialized aggregates，或者物化汇总）。

物化，可以简单理解为持久化。本质上是一种空间换时间的 tradeoff。

数据仓库查询通常涉及聚合函数，如 SQL 中的 COUNT、SUM、AVG、MIN 或 MAX。如果这些函数被多次用到，每次都即时计算显然存在巨大浪费。因此一个想法就是，能不能将其缓存起来。

其与关系数据库中的视图（View）区别在于，视图是虚拟的、逻辑存在的，只是对用户提供的一种抽象，是一个查询的中间结果，并没有进行持久化（有没有缓存就不知道了）。

物化视图本质上是对数据的一个摘要存储，如果原数据发生了变动，该视图要被重新生成。因此，如果写多读少，则维持物化视图的代价很大。但在数仓中往往反过来，因此物化视图才能较好的起作用。

物化视图一个特化的例子，是数据立方（data cube，或者 OLAP cube）：按不同维度对量化数据进行聚合。

ddia-3-12-data-cube.png

上图是一个按日期和产品分类两个维度进行加和的数据立方，当针对日期和产品进行汇总查询时，由于该表的存在，就会变得非常快。

当然，现实中，一个表中常常有多个维度，比如 3-9 中有日期、产品、商店、促销和客户五个维度。但构建数据立方的意义和方法都是相似的。

但这种构建出来的视图只能针对固定的查询进行优化，如果有的查询不在此列，则这些优化就不再起作用。

在实际中，需要针对性的识别（或者预估）每个场景查询分布，针对性的构建物化视图。