mirror of
https://github.com/LCTT/TranslateProject.git
synced 2025-01-10 22:21:11 +08:00
129 lines
9.2 KiB
Markdown
129 lines
9.2 KiB
Markdown
递归:梦中梦
|
||
======
|
||
|
||
> “方其梦也,不知其梦也。梦之中又占其梦焉,觉而后知其梦也。” —— 《庄子·齐物论》
|
||
|
||
**递归**是很神奇的,但是在大多数的编程类书藉中对递归讲解的并不好。它们只是给你展示一个递归阶乘的实现,然后警告你递归运行的很慢,并且还有可能因为栈缓冲区溢出而崩溃。“你可以将头伸进微波炉中去烘干你的头发,但是需要警惕颅内高压并让你的头发生爆炸,或者你可以使用毛巾来擦干头发。”难怪人们不愿意使用递归。但这种建议是很糟糕的,因为在算法中,递归是一个非常强大的思想。
|
||
|
||
我们来看一下这个经典的递归阶乘:
|
||
|
||
```
|
||
#include <stdio.h>
|
||
|
||
int factorial(int n)
|
||
{
|
||
int previous = 0xdeadbeef;
|
||
|
||
if (n == 0 || n == 1) {
|
||
return 1;
|
||
}
|
||
|
||
previous = factorial(n-1);
|
||
return n * previous;
|
||
}
|
||
|
||
int main(int argc)
|
||
{
|
||
int answer = factorial(5);
|
||
printf("%d\n", answer);
|
||
}
|
||
```
|
||
|
||
*递归阶乘 - factorial.c*
|
||
|
||
|
||
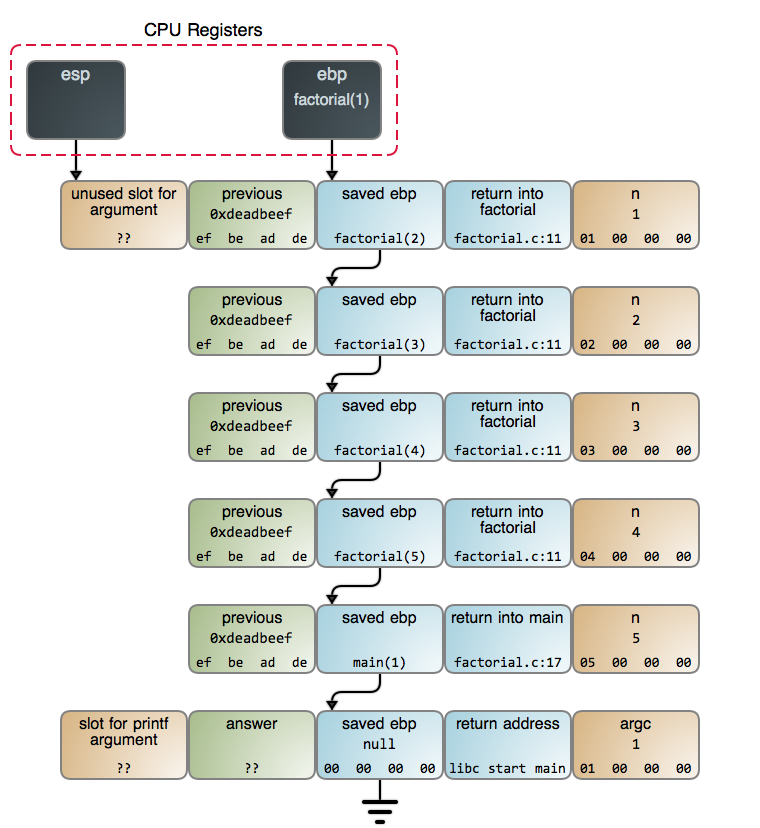
函数调用自身的这个观点在一开始是让人很难理解的。为了让这个过程更形象具体,下图展示的是当调用 `factorial(5)` 并且达到 `n == 1`这行代码 时,[栈上][3] 端点的情况:
|
||
|
||
|
||
|
||
每次调用 `factorial` 都生成一个新的 [栈帧][4]。这些栈帧的创建和 [销毁][5] 是使得递归版本的阶乘慢于其相应的迭代版本的原因。在调用返回之前,累积的这些栈帧可能会耗尽栈空间,进而使你的程序崩溃。
|
||
|
||
而这些担心经常是存在于理论上的。例如,对于每个 `factorial` 的栈帧占用 16 字节(这可能取决于栈排列以及其它因素)。如果在你的电脑上运行着现代的 x86 的 Linux 内核,一般情况下你拥有 8 GB 的栈空间,因此,`factorial` 程序中的 `n` 最多可以达到 512,000 左右。这是一个 [巨大无比的结果][6],它将花费 8,971,833 比特来表示这个结果,因此,栈空间根本就不是什么问题:一个极小的整数 —— 甚至是一个 64 位的整数 —— 在我们的栈空间被耗尽之前就早已经溢出了成千上万次了。
|
||
|
||
过一会儿我们再去看 CPU 的使用,现在,我们先从比特和字节回退一步,把递归看作一种通用技术。我们的阶乘算法可归结为:将整数 N、N-1、 … 1 推入到一个栈,然后将它们按相反的顺序相乘。实际上我们使用了程序调用栈来实现这一点,这是它的细节:我们在堆上分配一个栈并使用它。虽然调用栈具有特殊的特性,但是它也只是又一种数据结构而已,你可以随意使用。我希望这个示意图可以让你明白这一点。
|
||
|
||
当你将栈调用视为一种数据结构,有些事情将变得更加清晰明了:将那些整数堆积起来,然后再将它们相乘,这并不是一个好的想法。那是一种有缺陷的实现:就像你拿螺丝刀去钉钉子一样。相对更合理的是使用一个迭代过程去计算阶乘。
|
||
|
||
但是,螺丝钉太多了,我们只能挑一个。有一个经典的面试题,在迷宫里有一只老鼠,你必须帮助这只老鼠找到一个奶酪。假设老鼠能够在迷宫中向左或者向右转弯。你该怎么去建模来解决这个问题?
|
||
|
||
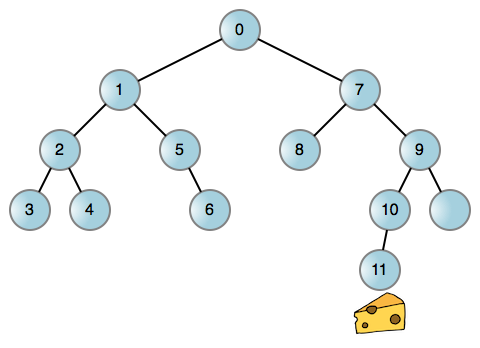
就像现实生活中的很多问题一样,你可以将这个老鼠找奶酪的问题简化为一个图,一个二叉树的每个结点代表在迷宫中的一个位置。然后你可以让老鼠在任何可能的地方都左转,而当它进入一个死胡同时,再回溯回去,再右转。这是一个老鼠行走的 [迷宫示例][7]:
|
||
|
||
|
||
|
||
每到边缘(线)都让老鼠左转或者右转来到达一个新的位置。如果向哪边转都被拦住,说明相关的边缘不存在。现在,我们来讨论一下!这个过程无论你是调用栈还是其它数据结构,它都离不开一个递归的过程。而使用调用栈是非常容易的:
|
||
|
||
|
||
```
|
||
#include <stdio.h>
|
||
#include "maze.h"
|
||
|
||
int explore(maze_t *node)
|
||
{
|
||
int found = 0;
|
||
|
||
if (node == NULL)
|
||
{
|
||
return 0;
|
||
}
|
||
if (node->hasCheese){
|
||
return 1;// found cheese
|
||
}
|
||
|
||
found = explore(node->left) || explore(node->right);
|
||
return found;
|
||
}
|
||
|
||
int main(int argc)
|
||
{
|
||
int found = explore(&maze);
|
||
}
|
||
```
|
||
|
||
*递归迷宫求解 [下载][2]*
|
||
|
||
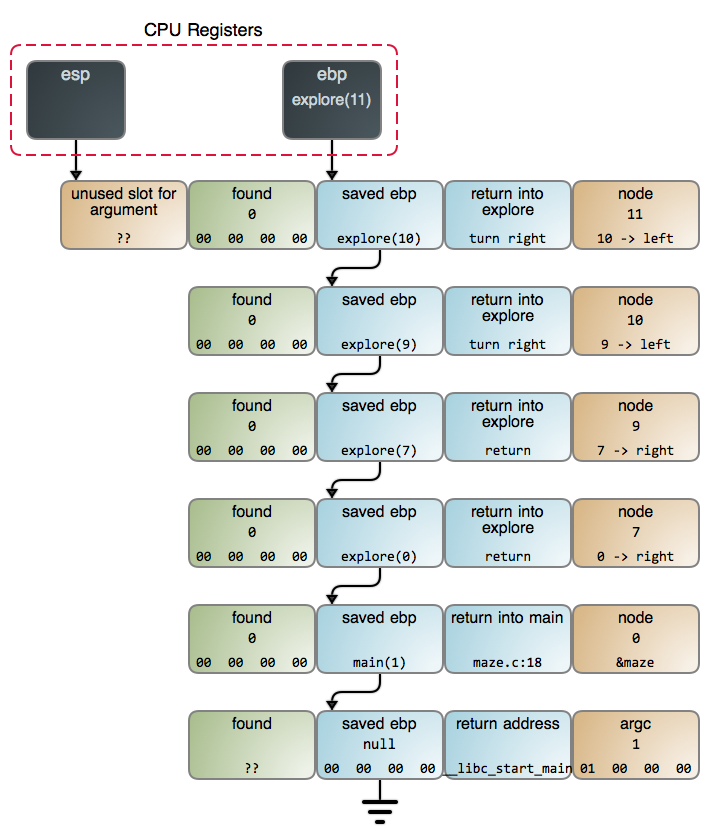
当我们在 `maze.c:13` 中找到奶酪时,栈的情况如下图所示。你也可以在 [GDB 输出][8] 中看到更详细的数据,它是使用 [命令][9] 采集的数据。
|
||
|
||
|
||
|
||
它展示了递归的良好表现,因为这是一个适合使用递归的问题。而且这并不奇怪:当涉及到算法时,*递归是规则,而不是例外*。它出现在如下情景中——进行搜索时、进行遍历树和其它数据结构时、进行解析时、需要排序时——它无处不在。正如众所周知的 pi 或者 e,它们在数学中像“神”一样的存在,因为它们是宇宙万物的基础,而递归也和它们一样:只是它存在于计算结构中。
|
||
|
||
Steven Skienna 的优秀著作 [算法设计指南][10] 的精彩之处在于,他通过 “战争故事” 作为手段来诠释工作,以此来展示解决现实世界中的问题背后的算法。这是我所知道的拓展你的算法知识的最佳资源。另一个读物是 McCarthy 的 [关于 LISP 实现的的原创论文][11]。递归在语言中既是它的名字也是它的基本原理。这篇论文既可读又有趣,在工作中能看到大师的作品是件让人兴奋的事情。
|
||
|
||
回到迷宫问题上。虽然它在这里很难离开递归,但是并不意味着必须通过调用栈的方式来实现。你可以使用像 `RRLL` 这样的字符串去跟踪转向,然后,依据这个字符串去决定老鼠下一步的动作。或者你可以分配一些其它的东西来记录追寻奶酪的整个状态。你仍然是实现了一个递归的过程,只是需要你实现一个自己的数据结构。
|
||
|
||
那样似乎更复杂一些,因为栈调用更合适。每个栈帧记录的不仅是当前节点,也记录那个节点上的计算状态(在这个案例中,我们是否只让它走左边,或者已经尝试向右)。因此,代码已经变得不重要了。然而,有时候我们因为害怕溢出和期望中的性能而放弃这种优秀的算法。那是很愚蠢的!
|
||
|
||
正如我们所见,栈空间是非常大的,在耗尽栈空间之前往往会遇到其它的限制。一方面可以通过检查问题大小来确保它能够被安全地处理。而对 CPU 的担心是由两个广为流传的有问题的示例所导致的:<ruby>哑阶乘<rt>dumb factorial</rt></ruby>和可怕的无记忆的 O( 2^n ) [Fibonacci 递归][12]。它们并不是栈递归算法的正确代表。
|
||
|
||
事实上栈操作是非常快的。通常,栈对数据的偏移是非常准确的,它在 [缓存][13] 中是热数据,并且是由专门的指令来操作它的。同时,使用你自己定义的在堆上分配的数据结构的相关开销是很大的。经常能看到人们写的一些比栈调用递归更复杂、性能更差的实现方法。最后,现代的 CPU 的性能都是 [非常好的][14] ,并且一般 CPU 不会是性能瓶颈所在。在考虑牺牲程序的简单性时要特别注意,就像经常考虑程序的性能及性能的[测量][15]那样。
|
||
|
||
下一篇文章将是探秘栈系列的最后一篇了,我们将了解尾调用、闭包、以及其它相关概念。然后,我们就该深入我们的老朋友—— Linux 内核了。感谢你的阅读!
|
||
|
||

|
||
|
||
--------------------------------------------------------------------------------
|
||
|
||
via:https://manybutfinite.com/post/recursion/
|
||
|
||
作者:[Gustavo Duarte][a]
|
||
译者:[qhwdw](https://github.com/qhwdw)
|
||
校对:[FSSlc](https://github.com/FSSlc)
|
||
|
||
本文由 [LCTT](https://github.com/LCTT/TranslateProject) 原创编译,[Linux中国](https://linux.cn/) 荣誉推出
|
||
|
||
[a]:http://duartes.org/gustavo/blog/about/
|
||
[1]:https://manybutfinite.com/post/recursion/
|
||
[2]:https://manybutfinite.com/code/x86-stack/maze.c
|
||
[3]:https://github.com/gduarte/blog/blob/master/code/x86-stack/factorial-gdb-output.txt
|
||
[4]:https://manybutfinite.com/post/journey-to-the-stack
|
||
[5]:https://manybutfinite.com/post/epilogues-canaries-buffer-overflows/
|
||
[6]:https://gist.github.com/gduarte/9944878
|
||
[7]:https://github.com/gduarte/blog/blob/master/code/x86-stack/maze.h
|
||
[8]:https://github.com/gduarte/blog/blob/master/code/x86-stack/maze-gdb-output.txt
|
||
[9]:https://github.com/gduarte/blog/blob/master/code/x86-stack/maze-gdb-commands.txt
|
||
[10]:http://www.amazon.com/Algorithm-Design-Manual-Steven-Skiena/dp/1848000693/
|
||
[11]:https://github.com/papers-we-love/papers-we-love/blob/master/comp_sci_fundamentals_and_history/recursive-functions-of-symbolic-expressions-and-their-computation-by-machine-parti.pdf
|
||
[12]:http://stackoverflow.com/questions/360748/computational-complexity-of-fibonacci-sequence
|
||
[13]:https://manybutfinite.com/post/intel-cpu-caches/
|
||
[14]:https://manybutfinite.com/post/what-your-computer-does-while-you-wait/
|
||
[15]:https://manybutfinite.com/post/performance-is-a-science |