mirror of
https://github.com/LCTT/TranslateProject.git
synced 2025-01-22 23:00:57 +08:00
112 lines
17 KiB
Markdown
112 lines
17 KiB
Markdown
密码学及公钥基础设施入门
|
||
======
|
||
|
||
> 学习密码学背后的基本概念,主要是保密性、完整性和身份认证。
|
||
|
||

|
||
|
||
安全通信正快速成为当今互联网的规范。从 2018 年 7 月起,Google Chrome 将对**全部**使用 HTTP 传输(而不是 HTTPS 传输)的站点[开始显示“不安全”警告][1]。虽然密码学已经逐渐变广为人知,但其本身并没有变得更容易理解。[Let's Encrypt][3] 设计并实现了一套令人惊叹的解决方案,可以提供免费安全证书和周期性续签;但如果不了解底层概念和缺陷,你也不过是加入了类似“[<ruby>货物崇拜<rt>cargo cult</rt></ruby>][4]”的技术崇拜的程序员大军。
|
||
|
||
### 安全通信的特性
|
||
|
||
密码学最直观明显的目标是<ruby>保密性<rt>confidentiality</rt></ruby>:<ruby>消息<rt>message</rt></ruby>传输过程中不会被窥探内容。为了保密性,我们对消息进行加密:对于给定消息,我们结合一个<ruby>密钥<rt>key</rt></ruby>生成一个无意义的乱码,只有通过相同的密钥逆转加密过程(即解密过程)才能将其转换为可读的消息。假设我们有两个朋友 [Alice 和 Bob][5],以及他们的<ruby>八卦<rt>nosy</rt></ruby>邻居 Eve。Alice 加密类似 "Eve 很讨厌" 的消息,将其发送给 Bob,期间不用担心 Eve 会窥探到这条消息的内容。
|
||
|
||
对于真正的安全通信,保密性是不够的。假如 Eve 收集了足够多 Alice 和 Bob 之间的消息,发现单词 “Eve” 被加密为 "Xyzzy"。除此之外,Eve 还知道 Alice 和 Bob 正在准备一个派对,Alice 会将访客名单发送给 Bob。如果 Eve 拦截了消息并将 “Xyzzy” 加到访客列表的末尾,那么她已经成功的破坏了这个派对。因此,Alice 和 Bob 需要他们之间的通信可以提供<ruby>完整性<rt>integrity</rt></ruby>:消息应该不会被篡改。
|
||
|
||
而且我们还有一个问题有待解决。假如 Eve 观察到 Bob 打开了标记为“来自 Alice”的信封,信封中包含一条来自 Alice 的消息“再买一加仑冰淇淋”。Eve 看到 Bob 外出,回家时带着冰淇淋,这样虽然 Eve 并不知道消息的完整内容,但她对消息有了大致的了解。Bob 将上述消息丢弃,但 Eve 找出了它并在下一周中的每一天都向 Bob 的邮箱中投递一封标记为“来自 Alice”的信封,内容拷贝自之前 Bob 丢弃的那封信。这样到了派对的时候,冰淇淋严重超量;派对当晚结束后,Bob 分发剩余的冰淇淋,Eve 带着免费的冰淇淋回到家。消息是加密的,完整性也没问题,但 Bob 被误导了,没有认出发信人的真实身份。<ruby>身份认证<rt>Authentication</rt></ruby>这个特性用于保证你正在通信的人的确是其声称的那样。
|
||
|
||
信息安全还有[其它特性][6],但保密性、完整性和身份验证是你必须了解的三大特性。
|
||
|
||
### 加密和加密算法
|
||
|
||
加密都包含哪些部分呢?首先,需要一条消息,我们称之为<ruby>明文<rt>plaintext</rt></ruby>。接着,需要对明文做一些格式上的初始化,以便用于后续的加密过程(例如,假如我们使用<ruby>分组加密算法<rt>block cipher</rt></ruby>,需要在明文尾部填充使其达到特定长度)。下一步,需要一个保密的比特序列,我们称之为<ruby>密钥<rt>key</rt></ruby>。然后,基于私钥,使用一种加密算法将明文转换为<ruby>密文<rt>ciphertext</rt></ruby>。密文看上去像是随机噪声,只有通过相同的加密算法和相同的密钥(在后面提到的非对称加密算法情况下,是另一个数学上相关的密钥)才能恢复为明文。
|
||
|
||
(LCTT 译注:cipher 一般被翻译为密码,但其具体表达的意思是加密算法,这里采用加密算法的翻译)
|
||
|
||
加密算法使用密钥加密明文。考虑到希望能够解密密文,我们用到的加密算法也必须是<ruby>可逆的<rt>reversible</rt></ruby>。作为简单示例,我们可以使用 [XOR][7]。该算子可逆,而且逆算子就是本身(`P ^ K = C; C ^ K = P`),故可同时用于加密和解密。该算子的平凡应用可以是<ruby>一次性密码本<rt>one-time pad</rt></ruby>,不过一般而言并不[可行][9]。但可以将 XOR 与一个基于单个密钥生成<ruby>任意随机数据流<rt>arbitrary stream of random data</rt></ruby>的函数结合起来。现代加密算法 AES 和 Chacha20 就是这么设计的。
|
||
|
||
我们把加密和解密使用同一个密钥的加密算法称为<ruby>对称加密算法<rt>symmetric cipher</rt></ruby>。对称加密算法分为<ruby>流加密算法<rt>stream ciphers</rt></ruby>和分组加密算法两类。流加密算法依次对明文中的每个比特或字节进行加密。例如,我们上面提到的 XOR 加密算法就是一个流加密算法。流加密算法适用于明文长度未知的情形,例如数据从管道或 socket 传入。[RC4][10] 是最为人知的流加密算法,但在多种不同的攻击面前比较脆弱,以至于最新版本 (1.3)的 TLS (“HTTPS” 中的 “S”)已经不再支持该加密算法。[Efforts][11] 正着手创建新的加密算法,候选算法 [ChaCha20][12] 已经被 TLS 支持。
|
||
|
||
分组加密算法对固定长度的分组,使用固定长度的密钥加密。在分组加密算法领域,排行第一的是 [<ruby>先进加密标准<rt>Advanced Encryption Standard</rt></ruby>][13](AES),使用的分组长度为 128 比特。分组包含的数据并不多,因而分组加密算法包含一个[工作模式][14],用于描述如何对任意长度的明文执行分组加密。最简单的工作模式是 [<ruby>电子密码本<rt>Electronic Code Book</rt></ruby>][15](ECB),将明文按分组大小划分成多个分组(在必要情况下,填充最后一个分组),使用密钥独立的加密各个分组。
|
||
|
||

|
||
|
||
这里我们留意到一个问题:如果相同的分组在明文中出现多次(例如互联网流量中的 `GET / HTTP/1.1` 词组),由于我们使用相同的密钥加密分组,我们会得到相同的加密结果。我们的安全通信中会出现一种<ruby>模式规律<rt>pattern</rt></ruby>,容易受到攻击。
|
||
|
||
因此还有很多高级的工作模式,例如 [<ruby>密码分组链接<rt>Cipher Block Chaining</rt></ruby>][16](CBC),其中每个分组的明文在加密前会与前一个分组的密文进行 XOR 操作,而第一个分组的明文与一个随机数构成的初始化向量进行 XOR 操作。还有其它一些工作模式,在安全性和执行速度方面各有优缺点。甚至还有 Counter (CTR) 这种工作模式,可以将分组加密算法转换为流加密算法。
|
||
|
||
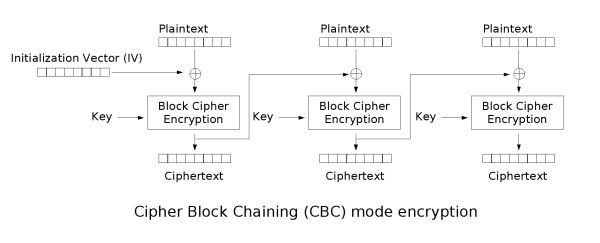
|
||
|
||
除了对称加密算法,还有<ruby>非对称加密算法<rt>asymmetric ciphers</rt></ruby>,也被称为<ruby>公钥密码学<rt>public-key cryptography</rt></ruby>。这类加密算法使用两个密钥:一个<ruby>公钥<rt>public key</rt></ruby>,一个<ruby>私钥<rt>private key</rt></ruby>。公钥和私钥在数学上有一定关联,但可以区分二者。经过公钥加密的密文只能通过私钥解密,经过私钥加密的密文可以通过公钥解密。公钥可以大范围分发出去,但私钥必须对外不可见。如果你希望和一个给定的人通信,你可以使用对方的公钥加密消息,这样只有他们的私钥可以解密出消息。在非对称加密算法领域,目前 [RSA][17] 最具有影响力。
|
||
|
||
非对称加密算法最主要的缺陷是,它们是<ruby>计算密集型<rt>computationally expensive</rt></ruby>的。那么使用对称加密算法可以让身份验证更快吗?如果你只与一个人共享密钥,答案是肯定的。但这种方式很快就会失效。假如一群人希望使用对称加密算法进行两两通信,如果对每对成员通信都采用单独的密钥,一个 20 人的群体将有 190 对成员通信,即每个成员要维护 19 个密钥并确认其安全性。如果使用非对称加密算法,每个成员仅需确保自己的私钥安全并维护一个公钥列表即可。
|
||
|
||
非对称加密算法也有加密[数据长度][18]限制。类似于分组加密算法,你需要将长消息进行划分。但实际应用中,非对称加密算法通常用于建立<ruby>机密<rt>confidential</rt></ruby>、<ruby>已认证<rt>authenticated</rt></ruby>的<ruby>通道<rt>channel</rt></ruby>,利用该通道交换对称加密算法的共享密钥。考虑到速度优势,对称加密算法用于后续的通信。TLS 就是严格按照这种方式运行的。
|
||
|
||
### 基础
|
||
|
||
安全通信的核心在于随机数。随机数用于生成密钥并为<ruby>确定性过程<rt>deterministic processes</rt></ruby>提供不可预测性。如果我们使用的密钥是可预测的,那我们从一开始就可能受到攻击。计算机被设计成按固定规则操作,因此生成随机数是比较困难的。计算机可以收集鼠标移动或<ruby>键盘计时<rt>keyboard timings</rt></ruby>这类随机数据。但收集随机性(也叫<ruby>信息熵<rt>entropy</rt></ruby>)需要花费不少时间,而且涉及额外处理以确保<ruby>均匀分布<rt>uniform distribution</rt></ruby>。甚至可以使用专用硬件,例如[<ruby>熔岩灯<rt>lava lamps</rt></ruby>墙][19]等。一般而言,一旦有了一个真正的随机数值,我们可以将其用作<ruby>种子<rt>seed</rt></ruby>,使用<ruby>密码安全的伪随机数生成器<rt>cryptographically secure pseudorandom number generator</rt></ruby>生成随机数。使用相同的种子,同一个随机数生成器生成的随机数序列保持不变,但重要的是随机数序列是无规律的。在 Linux 内核中,[/dev/random 和 /dev/urandom][21] 工作方式如下:从多个来源收集信息熵,进行<ruby>无偏处理<rt>remove biases</rt></ruby>,生成种子,然后生成随机数,该随机数可用于 RSA 密钥生成等。
|
||
|
||
### 其它密码学组件
|
||
|
||
我们已经实现了保密性,但还没有考虑完整性和身份验证。对于后两者,我们需要使用一些额外的技术。
|
||
|
||
首先是<ruby>密码散列函数<rt>crytographic hash function</rt></ruby>,该函数接受任意长度的输入并给出固定长度的输出(一般称为<ruby>摘要<rt>digest</rt></ruby>)。如果我们找到两条消息,其摘要相同,我们称之为<ruby>碰撞<rt>collision</rt></ruby>,对应的散列函数就不适合用于密码学。这里需要强调一下“找到”:考虑到消息的条数是无限的而摘要的长度是固定的,那么总是会存在碰撞;但如果无需海量的计算资源,我们总是能找到发生碰撞的消息对,那就令人比较担心了。更严重的情况是,对于每一个给定的消息,都能找到与之碰撞的另一条消息。
|
||
|
||
另外,哈希函数必须是<ruby>单向的<rt>one-way</rt></ruby>:给定一个摘要,反向计算对应的消息在计算上不可行。相应的,这类[条件][22]被称为<ruby>碰撞阻力<rt>collision resistance</rt></ruby>、<ruby>第二原象抗性<rt>second preimage resistance</rt></ruby>和<ruby>原象抗性<rt>preimage resistance</rt></ruby>。如果满足这些条件,摘要可以用作消息的指纹。[理论上][23]不存在具有相同指纹的两个人,而且你无法使用指纹反向找到其对应的人。
|
||
|
||
如果我们同时发送消息及其摘要,接收者可以使用相同的哈希函数独立计算摘要。如果两个摘要相同,可以认为消息没有被篡改。考虑到 [SHA-1][25] 已经变得[有些过时][26],目前最流行的密码散列函数是 [SHA-256][24]。
|
||
|
||
散列函数看起来不错,但如果有人可以同时篡改消息及其摘要,那么消息发送仍然是不安全的。我们需要将哈希与加密算法结合起来。在对称加密算法领域,我们有<ruby>消息认证码<rt>message authentication codes</rt></ruby>(MAC)技术。MAC 有多种形式,但<ruby>哈希消息认证码<rt>hash message authentication codes</rt></ruby>(HMAC) 这类是基于哈希的。[HMAC][27] 使用哈希函数 H 处理密钥 K、消息 M,公式为 `H(K + H(K + M))`,其中 `+` 代表<ruby>连接<rt>concatenation</rt></ruby>。公式的独特之处并不在本文讨论范围内,大致来说与保护 HMAC 自身的完整性有关。发送加密消息的同时也发送 MAC。Eve 可以任意篡改消息,但一旦 Bob 独立计算 MAC 并与接收到的 MAC 做比较,就会发现消息已经被篡改。
|
||
|
||
在非对称加密算法领域,我们有<ruby>数字签名<rt>digital signatures</rt></ruby>技术。如果使用 RSA,使用公钥加密的内容只能通过私钥解密,反过来也是如此;这种机制可用于创建一种签名。如果只有我持有私钥并用其加密文档,那么只有我的公钥可以用于解密,那么大家潜在的承认文档是我写的:这是一种身份验证。事实上,我们无需加密整个文档。如果生成文档的摘要,只要对这个指纹加密即可。对摘要签名比对整个文档签名要快得多,而且可以解决非对称加密存在的消息长度限制问题。接收者解密出摘要信息,独立计算消息的摘要并进行比对,可以确保消息的完整性。对于不同的非对称加密算法,数字签名的方法也各不相同;但核心都是使用公钥来检验已有签名。
|
||
|
||
### 汇总
|
||
|
||
现在,我们已经有了全部的主体组件,可以用其实现一个我们期待的、具有全部三个特性的[<ruby>体系<rt>system</rt></ruby>][28]。Alice 选取一个保密的对称加密密钥并使用 Bob 的公钥进行加密。接着,她对得到的密文进行哈希并使用其私钥对摘要进行签名。Bob 接收到密文和签名,一方面独立计算密文的摘要,另一方面使用 Alice 的公钥解密签名中的摘要;如果两个摘要相同,他可以确信对称加密密钥没有被篡改且通过了身份验证。Bob 使用私钥解密密文得到对称加密密钥,接着使用该密钥及 HMAC 与 Alice 进行保密通信,这样每一条消息的完整性都得到保障。但该体系没有办法抵御消息重放攻击(我们在 Eve 造成的冰淇淋灾难中见过这种攻击)。要解决重放攻击,我们需要使用某种类型的“<ruby>握手<rt>handshake</rt></ruby>”建立随机、短期的<ruby>会话标识符<rt>session identifier</rt></ruby>。
|
||
|
||
密码学的世界博大精深,我希望这篇文章能让你对密码学的核心目标及其组件有一个大致的了解。这些概念为你打下坚实的基础,让你可以继续深入学习。
|
||
|
||
感谢 Hubert Kario、Florian Weimer 和 Mike Bursell 在本文写作过程中提供的帮助。
|
||
|
||
--------------------------------------------------------------------------------
|
||
|
||
via: https://opensource.com/article/18/5/cryptography-pki
|
||
|
||
作者:[Alex Wood][a]
|
||
选题:[lujun9972](https://github.com/lujun9972)
|
||
译者:[pinewall](https://github.com/pinewall)
|
||
校对:[wxy](https://github.com/wxy)
|
||
|
||
本文由 [LCTT](https://github.com/LCTT/TranslateProject) 原创编译,[Linux中国](https://linux.cn/) 荣誉推出
|
||
|
||
[a]:https://opensource.com/users/awood
|
||
[1]:https://security.googleblog.com/2018/02/a-secure-web-is-here-to-stay.html
|
||
[2]:https://blog.mozilla.org/security/2017/01/20/communicating-the-dangers-of-non-secure-http/
|
||
[3]:https://letsencrypt.org/
|
||
[4]:https://en.wikipedia.org/wiki/Cargo_cult_programming
|
||
[5]:https://en.wikipedia.org/wiki/Alice_and_Bob
|
||
[6]:https://en.wikipedia.org/wiki/Information_security#Availability
|
||
[7]:https://en.wikipedia.org/wiki/XOR_cipher
|
||
[8]:https://en.wikipedia.org/wiki/Involution_(mathematics)#Computer_science
|
||
[9]:https://en.wikipedia.org/wiki/One-time_pad#Problems
|
||
[10]:https://en.wikipedia.org/wiki/RC4
|
||
[11]:https://en.wikipedia.org/wiki/ESTREAM
|
||
[12]:https://en.wikipedia.org/wiki/Salsa20
|
||
[13]:https://en.wikipedia.org/wiki/Advanced_Encryption_Standard
|
||
[14]:https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation
|
||
[15]:https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation#/media/File:ECB_encryption.svg
|
||
[16]:https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation#/media/File:CBC_encryption.svg
|
||
[17]:https://en.wikipedia.org/wiki/RSA_(cryptosystem)
|
||
[18]:https://security.stackexchange.com/questions/33434/rsa-maximum-bytes-to-encrypt-comparison-to-aes-in-terms-of-security
|
||
[19]:https://www.youtube.com/watch?v=1cUUfMeOijg
|
||
[20]:https://en.wikipedia.org/wiki/Cryptographically_secure_pseudorandom_number_generator
|
||
[21]:https://www.2uo.de/myths-about-urandom/
|
||
[22]:https://crypto.stackexchange.com/a/1174
|
||
[23]:https://www.telegraph.co.uk/science/2016/03/14/why-your-fingerprints-may-not-be-unique/
|
||
[24]:https://en.wikipedia.org/wiki/SHA-2
|
||
[25]:https://en.wikipedia.org/wiki/SHA-1
|
||
[26]:https://security.googleblog.com/2017/02/announcing-first-sha1-collision.html
|
||
[27]:https://en.wikipedia.org/wiki/HMAC
|
||
[28]:https://en.wikipedia.org/wiki/Hybrid_cryptosystem
|