10 KiB
ZOMBIES:为什么简洁性是交付健壮软件的关键(五)
当你坚持最简场景时,你最终会得到最简单的解决方案。
在前面的文章中,我已经解释了为什么将编程问题看作一整群丧尸来处理是错误的。我用 ZOMBIES 方法来解释为什么循序渐进地处理问题更好。
ZOMBIES 表示以下首字母缩写:
- Z – 最简场景(Zero)
- O – 单元素场景(One)
- M – 多元素场景(Many or more complex)
- B – 边界行为(Boundary behaviors)
- I – 接口定义(Interface definition)
- E – 处理特殊行为(Exercise exceptional behavior)
- S – 简单场景用简单的解决方案(Simple scenarios, simple solutions)
在系列的前四篇文章中,我展示了 ZOMBIES 方法的前六个原则(LCTT译注:原文为前五个,应为笔误)。
第一篇中 实现了最简场景,它为代码提供了最简可行路径。第二篇文章中执行了 单元素场景和多元素场景上的测试。第三篇中介绍了 边界和接口。 第四篇中处理 特殊行为。在本文中,我将介绍最后一项:简单场景用简单的解决方案。
简单场景用简单的解决方案
回顾这个网购 API 的实现过程,你会发现总是有目的性地坚持考虑最简单的场景。在这个过程中,最终你会得到最简单的解决方案。
ZOMBIES 方法通过坚持简洁性来帮助你交付健壮优雅的解决方案。
胜利了吗?
似乎一切工作都结束了,一个不那么认真负责的工程师很可能会宣布胜利。但开明的工程师总是会探索得更深一点。
我一直推荐做 变异测试。在圆满结束这个练习项目,开始新的征程之前,用变异测试来敲打敲打你的解决方案是明智的。况且你也不得不承认,变异很适合对付丧尸的。
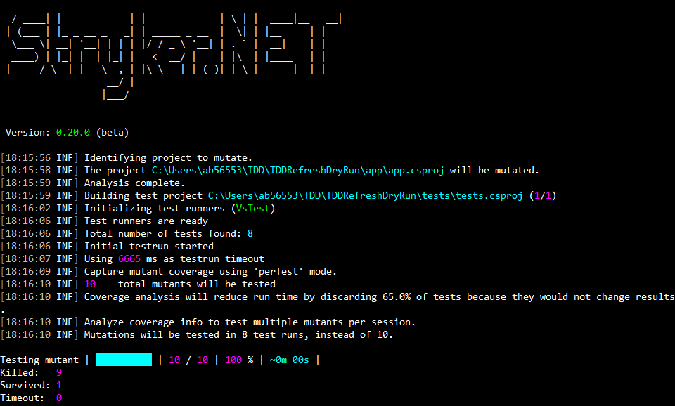
你可以在开源网站 Stryker.NET 上进行变异测试。
看起来有一个存活的变异体。这可不是好兆头。
这意味着什么呢?当你自认为解决方案无懈可击的时候,Stryker.NET 却表示在你的地盘上并非一切安好。
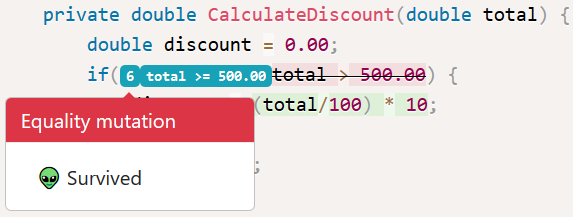
让我们来看看这个存活下来的烦人变异体:
变异测试工具将
if(total > 500.00) {
变异为:
if(total >= 500.00) {
然后运行测试,结果对于这个变化没有一个测试失败。如果业务处理代码中发生了一处变动却没有任何一个测试失败,这就意味着你遇到一个存活的变异体。
为什么要在意变异体
为什么存活的变异体是麻烦的征兆呢?因为你写的业务处理逻辑代码控制着整个系统的行为。如果业务处理逻辑改变,系统的行为也应该随之改变。而系统行为的改变应该会导致测试表示的期望被违反。如果没有期望被违反,那就说明这些期望对系统行为的描述还不够准确。这也意味着你的业务处理逻辑中存在漏洞。
要解决这个问题,你需要干掉这个存活下来的变异体。要怎么做呢?一般来说,有存活的变异体意味着有期望被遗漏了。
仔细检查代码,梳理已定义的期望,看看漏掉了什么:
- 期望 0:新建购物框里有零个商品(这隐含了总价为 ¥0)。
- 期望 1:向购物框添加一件商品的结果是购物框里有一件商品,如果这件商品的价格是 ¥10,那么总价为 ¥10。
- 期望 2:向购物框添里加入一件价值 ¥10 的商品,再加入一件价值 ¥20 的商品,总价是 ¥30 。
- 期望 3:关于从购物框移除商品的期望。
- 期望 4:总价大于 ¥500 时打,享受九折优惠。
缺了什么呢?根据变异测试报告,你没有定义订单总价刚好为 ¥500 的销售策略。你已经定义订单总额大于 ¥500 和小于 ¥500 时的情况。
定义边界情况的期望:
[Fact]
public void Add2ItemsTotal500GrandTotal500() {
var expectedGrandTotal = 500.00;
var actualGrandTotal = 450;
Assert.Equal(expectedGrandTotal, actualGrandTotal);
}
第一步先写一个假的实现让测试失败。现在共有 9 个微测试。其中 8 个通过,第 9 个失败了:
[xUnit.net 00:00:00.57] tests.UnitTest1.Add2ItemsTotal500GrandTotal500 [FAIL]
X tests.UnitTest1.Add2ItemsTotal500GrandTotal500 [2ms]
Error Message:
Assert.Equal() Failure
Expected: 500
Actual: 450
[...]
Test Run Failed.
Total tests: 9
Passed: 8
Failed: 1
Total time: 1.5920 Seconds
将硬编码值替换成正样例的预期代码:
[Fact]
public void Add2ItemsTotal500GrandTotal500() {
var expectedGrandTotal = 500.00;
Hashtable item1 = new Hashtable();
item1.Add("0001", 400.00);
shoppingAPI.AddItem(item1);
Hashtable item2 = new Hashtable();
item2.Add("0002", 100.00);
shoppingAPI.AddItem(item2);
var actualGrandTotal = shoppingAPI.CalculateGrandTotal(); }
共添加了两件商品,一件价值 ¥400,另一件价值 ¥100,总价是 ¥500。调用计算总价的函数,期望的总价是 ¥500。
运行,9 个测试全部通过!
Total tests: 9
Passed: 9
Failed: 0
Total time: 1.0440 Seconds
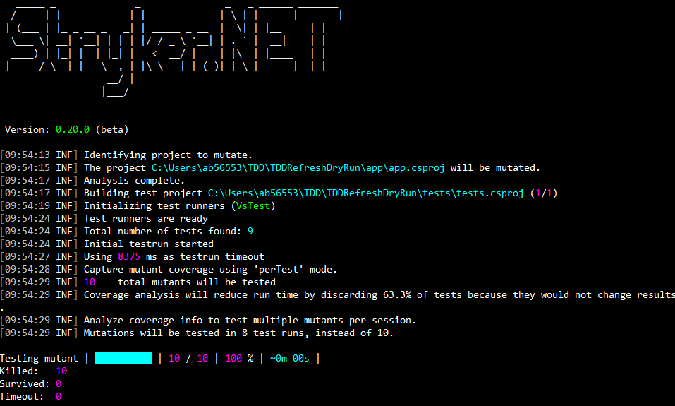
现在是揭晓真相的时刻。这个新增的期望能够清理掉所有的变异体吗?运行变异测试来看看结果:
成功了!10 个变异体全都被干掉了。太棒了!现在你可以放心地发布这个 API 了。
结语
如果从这次练习中有什么收获的话,那就是 技术性拖延 这一概念的提出。这个是一个重要的概念,因为我们中的许多人往往会在客户描述完他们的问题之前,就盲目地去设想解决方案。
主动拖延
拖延对于软件工程师来说并不是一件容易的事情。我们总是急于动手写代码。我们熟悉各种设计模式、反模式、编程原则和现成的解决方案。我们总是迫不及待想将它们应用到可执行的代码中,并且倾向于一次性做大量的工作。所以在行动之前仔细考虑每个步骤是一种美德。
这个练习说明 ZOMBIES 方法能够通过一系列深思熟虑的小步骤来帮你实现解决方案。但是有一点需要特别注意,根据 Yagni 原则,这些深思熟虑常常会飞得太远,以至于最终形成一个大而全的系统。这会产生臃肿、紧密耦合的系统。
迭代式开发与增量式开发
在这次练习给我们的另一个重要收获是让我们意识到保持系统持续可用的唯一方法是采用迭代式的开发方法。你通过改造已有代码开发出整个购物 API。这种改造工作是在迭代优化解决方案的过程中不可避免的。
很多团队混淆了迭代和增量。这是两个完全不同的概念。
增量式方法是假设是你有完整清晰的需求,然后通过增量累加的方式来构建解方案。大体上来说,你一点点地构建各个部分,然后将所有的部分组装在一起。大功告成!解决方案已经准备好交付了!
相比之下,迭代式方法中,你并不很确定自己需要交付给客户的是什么。因为这个原因,你更加小心谨慎。你会小心翼翼地避免破坏能够运行的系统(也就是说系统处于稳态)。如果不得不扰动已有的平衡,你也会采取最小侵入性的方式。你专注于用尽可能小的工作量来快速完成每次得改动工作。你倾向于让系统尽快回到稳态。
这就是为什么迭代式方法在真正实现一个功能之前总是先提供一个假实现。你硬编码一系列的期望,以验证小的修改不会导致系统无法运行。然后进行必要的修改,用实际处理代码替换硬编码的值。
作为经验法则,在迭代方法中,你的目标是通过设计期望(微测试),对代码进行不断改进。每进行一次改进,你都要检验系统,以确保它处于工作状态。以这种方式不断前进,最终会达到满足所有期望的程度,并且此时代码已经被重构,没有任何存活的变异体了。
一旦达到了这种状态,你就可以相当自信地交付解决方案了。
由衷感谢 Kent Beck、 Ron Jeffries 和GeePaw Hill 在我的软件工程学习道路的启发。
愿 ZOMBIES 方法在软件开发的征程上帮助到你。
(题图:MJ/ca463fc6-021b-4818-ba3d-9cd3c8736577)
via: https://opensource.com/article/21/2/simplicity
作者:Alex Bunardzic 选题:lkxed 译者:toknow-gh 校对:wxy