35 KiB
JavaScript 函数式编程介绍
探索函数式编程,通过它让你的程序更具有可读性和易于调试
Image credits : Steve Jurvetson via Flickr (CC-BY-2.0)
当 Brendan Eich 在 1995 年创造 JavaScript 时,他原本打算将 Scheme 移植到浏览器里 。Scheme 作为 Lisp 的方言,是一种函数式编程语言。而当 Eich 被告知新的语言应该是一种可以与 Java 相比的脚本语言后,他最终确立了一种拥有 C 风格语法的语言(也和 Java 一样),但将函数视作一等公民。而 Java 直到版本 8 才从技术上将函数视为一等公民,虽然你可以用匿名类来模拟它。这个特性允许 JavaScript 通过函数式范式编程。
JavaScript 是一个多范式语言,允许你自由地混合和使用面向对象式、过程式和函数式的编程范式。最近,函数式编程越来越火热。在诸如 Angular 和 React 这样的框架中,通过使用不可变数据结构可以切实提高性能。不可变是函数式编程的核心原则,它以及纯函数使得编写和调试程序变得更加容易。使用函数来代替程序的循环可以提高程序的可读性并使它更加优雅。总之,函数式编程拥有很多优点。
什么不是函数式编程
在讨论什么是函数式编程前,让我们先排除那些不属于函数式编程的东西。实际上它们是你需要丢弃的语言组件(再见,老朋友):
- 循环:
whiledo...whileforfor...offor...in
- 用
var或者let来声明变量 - 没有返回值的函数
- 改变对象的属性 (比如:
o.x = 5;) - 改变数组本身的方法:
copyWithinfillpoppushreverseshiftsortspliceunshift
- 改变映射本身的方法:
cleardeleteset
- 改变集合本身的方法:
addcleardelete
脱离这些特性应该如何编写程序呢?这是我们将在后面探索的问题。
纯函数
你的程序中包含函数不一定意味着你正在进行函数式编程。函数式范式将纯函数和非纯函数区分开。鼓励你编写纯函数。纯函数必须满足下面的两个属性:
- 引用透明:函数在传入相同的参数后永远返回相同的返回值。这意味着该函数不依赖于任何可变状态。
- 无副作用:函数不能导致任何副作用。副作用可能包括 I/O(比如向终端或者日志文件写入),改变一个不可变的对象,对变量重新赋值等等。
我们来看一些例子。首先,multiply 就是一个纯函数的例子,它在传入相同的参数后永远返回相同的返回值,并且不会导致副作用。
function multiply(a, b) {
return a * b;
}
下面是非纯函数的例子。canRide 函数依赖捕获的 heightRequirement 变量。被捕获的变量不一定导致一个函数是非纯函数,除非它是一个可变的变量(或者可以被重新赋值)。这种情况下使用 let 来声明这个变量,意味着可以对它重新赋值。multiply 函数是非纯函数,因为它会导致在 console 上输出。
let heightRequirement = 46;
// Impure because it relies on a mutable (reassignable) variable.
function canRide(height) {
return height >= heightRequirement;
}
// Impure because it causes a side-effect by logging to the console.
function multiply(a, b) {
console.log('Arguments: ', a, b);
return a * b;
}
下面的列表包含着 JavaScript 内置的非纯函数。你可以指出它们不满足两个属性中的哪个吗?
console.logelement.addEventListenerMath.randomDate.now$.ajax(这里$代表你使用的 Ajax 库)
理想的程序中所有的函数都是纯函数,但是从上面的函数列表可以看出,任何有意义的程序都将包含非纯函数。大多时候我们需要进行 AJAX 调用,检查当前日期或者获取一个随机数。一个好的经验法则是遵循 80/20 规则:函数中有 80% 应该是纯函数,剩下的 20% 的必要性将不可避免地是非纯函数。
使用纯函数有几个优点:
- 它们很容易导出和调试,因为它们不依赖于可变的状态。
- 返回值可以被缓存或者“记忆”来避免以后重复计算。
- 它们很容易测试,因为没有需要模拟(mock)的依赖(比如日志,AJAX,数据库等等)。
你编写或者使用的函数返回空(换句话说它没有返回值),那代表它是非纯函数。
不变性
让我们回到捕获变量的概念上。来看看 canRide 函数。我们认为它是一个非纯函数,因为 heightRequirement 变量可以被重新赋值。下面是一个构造出来的例子来说明如何用不可预测的值来对它重新赋值。
let heightRequirement = 46;
function canRide(height) {
return height >= heightRequirement;
}
// Every half second, set heightRequirement to a random number between 0 and 200.
setInterval(() => heightRequirement = Math.floor(Math.random() * 201), 500);
const mySonsHeight = 47;
// Every half second, check if my son can ride.
// Sometimes it will be true and sometimes it will be false.
setInterval(() => console.log(canRide(mySonsHeight)), 500);
我要再次强调被捕获的变量不一定会使函数成为非纯函数。我们可以通过只是简单地改变 heightRequirement 的声明方式来使 canRide 函数成为纯函数。
const heightRequirement = 46;
function canRide(height) {
return height >= heightRequirement;
}
通过用 const 来声明变量意味着它不能被再次赋值。如果尝试对它重新赋值,运行时引擎将抛出错误;那么,如果用对象来代替数字来存储所有的“常量”怎么样?
const constants = {
heightRequirement: 46,
// ... other constants go here
};
function canRide(height) {
return height >= constants.heightRequirement;
}
我们用了 const ,所以这个变量不能被重新赋值,但是还有一个问题:这个对象可以被改变。下面的代码展示了,为了真正使其不可变,你不仅需要防止它被重新赋值,你也需要不可变的数据结构。JavaScript 语言提供了 Object.freeze 方法来阻止对象被改变。
'use strict';
// CASE 1: 对象的属性是可变的,并且变量可以被再次赋值。
let o1 = { foo: 'bar' };
// 改变对象的属性
o1.foo = 'something different';
// 对变量再次赋值
o1 = { message: "I'm a completely new object" };
// CASE 2: 对象的属性还是可变的,但是变量不能被再次赋值。
const o2 = { foo: 'baz' };
// 仍然能改变对象
o2.foo = 'Something different, yet again';
// 不能对变量再次赋值
// o2 = { message: 'I will cause an error if you uncomment me' }; // Error!
// CASE 3: 对象的属性是不可变的,但是变量可以被再次赋值。
let o3 = Object.freeze({ foo: "Can't mutate me" });
// 不能改变对象的属性
// o3.foo = 'Come on, uncomment me. I dare ya!'; // Error!
// 还是可以对变量再次赋值
o3 = { message: "I'm some other object, and I'm even mutable -- so take that!" };
// CASE 4: 对象的属性是不可变的,并且变量不能被再次赋值。这是我们想要的!!!!!!!!
const o4 = Object.freeze({ foo: 'never going to change me' });
// 不能改变对象的属性
// o4.foo = 'talk to the hand' // Error!
// 不能对变量再次赋值
// o4 = { message: "ain't gonna happen, sorry" }; // Error
不变性适用于所有的数据结构,包括数组、映射和集合。它意味着不能调用例如 Array.prototype.push 等会导致本身改变的方法,因为它会改变已经存在的数组。可以通过创建一个含有原来元素和新加元素的新数组,而不是将新元素加入一个已经存在的数组。其实所有会导致数组本身被修改的方法都可以通过一个返回修改好的新数组的函数代替。
'use strict';
const a = Object.freeze([4, 5, 6]);
// Instead of: a.push(7, 8, 9);
const b = a.concat(7, 8, 9);
// Instead of: a.pop();
const c = a.slice(0, -1);
// Instead of: a.unshift(1, 2, 3);
const d = [1, 2, 3].concat(a);
// Instead of: a.shift();
const e = a.slice(1);
// Instead of: a.sort(myCompareFunction);
const f = R.sort(myCompareFunction, a); // R = Ramda
// Instead of: a.reverse();
const g = R.reverse(a); // R = Ramda
// 留给读者的练习:
// copyWithin
// fill
// splice
映射 和 集合 也很相似。可以通过返回一个新的修改好的映射或者集合来代替使用会修改其本身的函数。
const map = new Map([
[1, 'one'],
[2, 'two'],
[3, 'three']
]);
// Instead of: map.set(4, 'four');
const map2 = new Map([...map, [4, 'four']]);
// Instead of: map.delete(1);
const map3 = new Map([...map].filter(([key]) => key !== 1));
// Instead of: map.clear();
const map4 = new Map();
const set = new Set(['A', 'B', 'C']);
// Instead of: set.add('D');
const set2 = new Set([...set, 'D']);
// Instead of: set.delete('B');
const set3 = new Set([...set].filter(key => key !== 'B'));
// Instead of: set.clear();
const set4 = new Set();
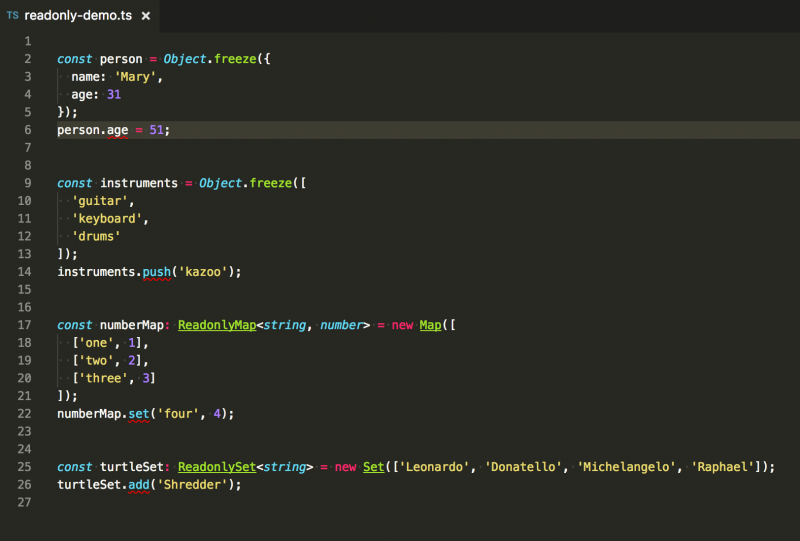
我想提一句如果你在使用 TypeScript(我非常喜欢 TypeScript),你可以用 Readonly<T>、ReadonlyArray<T>、ReadonlyMap<K, V> 和 ReadonlySet<T> 接口来在编译期检查你是否尝试更改这些对象,有则抛出编译错误。如果在对一个对象字面量或者数组调用 Object.freeze,编译器会自动推断它是只读的。由于映射和集合在其内部表达,所以在这些数据结构上调用 Object.freeze 不起作用。但是你可以轻松地告诉编译器它们是只读的变量。
TypeScript 只读接口
好,所以我们可以通过创建新的对象来代替修改原来的对象,但是这样不会导致性能损失吗?当然会。确保在你自己的应用中做了性能测试。如果你需要提高性能,可以考虑使用 Immutable.js。Immutable.js 用持久的数据结构 实现了链表、堆栈、映射、集合和其他数据结构。使用了如同 Clojure 和 Scala 这样的函数式语言中相同的技术。
// Use in place of `[]`.
const list1 = Immutable.List(['A', 'B', 'C']);
const list2 = list1.push('D', 'E');
console.log([...list1]); // ['A', 'B', 'C']
console.log([...list2]); // ['A', 'B', 'C', 'D', 'E']
// Use in place of `new Map()`
const map1 = Immutable.Map([
['one', 1],
['two', 2],
['three', 3]
]);
const map2 = map1.set('four', 4);
console.log([...map1]); // [['one', 1], ['two', 2], ['three', 3]]
console.log([...map2]); // [['one', 1], ['two', 2], ['three', 3], ['four', 4]]
// Use in place of `new Set()`
const set1 = Immutable.Set([1, 2, 3, 3, 3, 3, 3, 4]);
const set2 = set1.add(5);
console.log([...set1]); // [1, 2, 3, 4]
console.log([...set2]); // [1, 2, 3, 4, 5]
函数组合
记不记得在中学时我们学过一些像 (f ∘ g)(x) 的东西?你那时可能想,“我什么时候会用到这些?”,好了,现在就用到了。你准备好了吗?f ∘ g读作 “函数 f 和函数 g 组合”。对它的理解有两种等价的方式,如等式所示: (f ∘ g)(x) = f(g(x))。你可以认为 f ∘ g 是一个单独的函数,或者视作将调用函数 g 的结果作为参数传给函数 f。注意这些函数是从右向左依次调用的,先执行 g,接下来执行 f。
关于函数组合的几个要点:
- 我们可以组合任意数量的函数(不仅限于 2 个)。
- 组合函数的一个方式是简单地把一个函数的输出作为下一个函数的输入(比如
f(g(x)))。
// h(x) = x + 1
// number -> number
function h(x) {
return x + 1;
}
// g(x) = x^2
// number -> number
function g(x) {
return x * x;
}
// f(x) = convert x to string
// number -> string
function f(x) {
return x.toString();
}
// y = (f ∘ g ∘ h)(1)
const y = f(g(h(1)));
console.log(y); // '4'
Ramda 和 lodash 之类的库提供了更优雅的方式来组合函数。我们可以在更多的在数学意义上处理函数组合,而不是简单地将一个函数的返回值传递给下一个函数。我们可以创建一个由这些函数组成的单一复合函数(就是 (f ∘ g)(x))。
// h(x) = x + 1
// number -> number
function h(x) {
return x + 1;
}
// g(x) = x^2
// number -> number
function g(x) {
return x * x;
}
// f(x) = convert x to string
// number -> string
function f(x) {
return x.toString();
}
// R = Ramda
// composite = (f ∘ g ∘ h)
const composite = R.compose(f, g, h);
// Execute single function to get the result.
const y = composite(1);
console.log(y); // '4'
好了,我们可以在 JavaScript 中组合函数了。接下来呢?好,如果你已经入门了函数式编程,理想中你的程序将只有函数的组合。代码里没有循环(for, for...of, for...in, while, do),基本没有。你可能觉得那是不可能的。并不是这样。我们下面的两个话题是:递归和高阶函数。
递归
假设你想实现一个计算数字的阶乘的函数。 让我们回顾一下数学中阶乘的定义:
n! = n * (n-1) * (n-2) * ... * 1.
n! 是从 n 到 1 的所有整数的乘积。我们可以编写一个循环轻松地计算出结果。
function iterativeFactorial(n) {
let product = 1;
for (let i = 1; i <= n; i++) {
product *= i;
}
return product;
}
注意 product 和 i 都在循环中被反复重新赋值。这是解决这个问题的标准过程式方法。如何用函数式的方法解决这个问题呢?我们需要消除循环,确保没有变量被重新赋值。递归是函数式程序员的最有力的工具之一。递归需要我们将整体问题分解为类似整体问题的子问题。
计算阶乘是一个很好的例子,为了计算 n! 我们需要将 n 乘以所有比它小的正整数。它的意思就相当于:
n! = n * (n-1)!
啊哈!我们发现了一个解决 (n-1)! 的子问题,它类似于整个问题 n!。还有一个需要注意的地方就是基础条件。基础条件告诉我们何时停止递归。 如果我们没有基础条件,那么递归将永远持续。 实际上,如果有太多的递归调用,程序会抛出一个堆栈溢出错误。啊哈!
function recursiveFactorial(n) {
// Base case -- stop the recursion
if (n === 0) {
return 1; // 0! is defined to be 1.
}
return n * recursiveFactorial(n - 1);
}
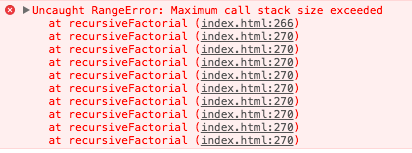
然后我们来计算 recursiveFactorial(20000) 因为……,为什么不呢?当我们这样做的时候,我们得到了这个结果:
堆栈溢出错误
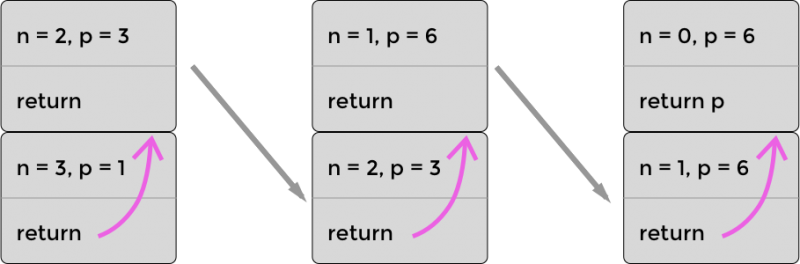
这里发生了什么?我们得到一个堆栈溢出错误!这不是无穷的递归导致的。我们已经处理了基础条件(n === 0 的情况)。那是因为浏览器的堆栈大小是有限的,而我们的代码使用了越过了这个大小的堆栈。每次对 recursiveFactorial 的调用导致了新的帧被压入堆栈中,就像一个盒子压在另一个盒子上。每当 recursiveFactorial 被调用,一个新的盒子被放在最上面。下图展示了在计算 recursiveFactorial(3) 时堆栈的样子。注意在真实的堆栈中,堆栈顶部的帧将存储在执行完成后应该返回的内存地址,但是我选择用变量 r 来表示返回值,因为 JavaScript 开发者一般不需要考虑内存地址。
递归计算 3! 的堆栈(三次乘法)
你可能会想象当计算 n = 20000 时堆栈会更高。我们可以做些什么优化它吗?当然可以。作为 ES2015 (又名 ES6) 标准的一部分,有一个优化用来解决这个问题。它被称作尾调用优化(PTC)。当递归函数做的最后一件事是调用自己并返回结果的时候,它使得浏览器删除或者忽略堆栈帧。实际上,这个优化对于相互递归函数也是有效的,但是为了简单起见,我们还是来看单一递归函数。
你可能会注意到,在递归函数调用之后,还要进行一次额外的计算(n * r)。那意味着浏览器不能通过 PTC 来优化递归;然而,我们可以通过重写函数使最后一步变成递归调用以便优化。一个窍门是将中间结果(在这里是 product)作为参数传递给函数。
'use strict';
// Optimized for tail call optimization.
function factorial(n, product = 1) {
if (n === 0) {
return product;
}
return factorial(n - 1, product * n)
}
让我们来看看优化后的计算 factorial(3) 时的堆栈。如下图所示,堆栈不会增长到超过两层。原因是我们把必要的信息都传到了递归函数中(比如 product)。所以,在 product 被更新后,浏览器可以丢弃掉堆栈中原先的帧。你可以在图中看到每次最上面的帧下沉变成了底部的帧,原先底部的帧被丢弃,因为不再需要它了。
递归计算 3! 的堆栈(三次乘法)使用 PTC
现在选一个浏览器运行吧,假设你在使用 Safari,你会得到 Infinity(它是比在 JavaScript 中能表达的最大值更大的数)。但是我们没有得到堆栈溢出错误,那很不错!现在在其他的浏览器中呢怎么样呢?Safari 可能现在乃至将来是实现 PTC 的唯一一个浏览器。看看下面的兼容性表格:
PTC 兼容性
其他浏览器提出了一种被称作语法级尾调用(STC)的竞争标准。“语法级”意味着你需要用新的语法来标识你想要执行尾递归优化的函数。即使浏览器还没有广泛支持,但是把你的递归函数写成支持尾递归优化的样子还是一个好主意。
高阶函数
我们已经知道 JavaScript 将函数视作一等公民,可以把函数像其他值一样传递。所以,把一个函数传给另一个函数也很常见。我们也可以让函数返回一个函数。就是它!我们有高阶函数。你可能已经很熟悉几个在 Array.prototype 中的高阶函数。比如 filter、map 和 reduce 就在其中。对高阶函数的一种理解是:它是接受(一般会调用)一个回调函数参数的函数。让我们来看看一些内置的高阶函数的例子:
const vehicles = [
{ make: 'Honda', model: 'CR-V', type: 'suv', price: 24045 },
{ make: 'Honda', model: 'Accord', type: 'sedan', price: 22455 },
{ make: 'Mazda', model: 'Mazda 6', type: 'sedan', price: 24195 },
{ make: 'Mazda', model: 'CX-9', type: 'suv', price: 31520 },
{ make: 'Toyota', model: '4Runner', type: 'suv', price: 34210 },
{ make: 'Toyota', model: 'Sequoia', type: 'suv', price: 45560 },
{ make: 'Toyota', model: 'Tacoma', type: 'truck', price: 24320 },
{ make: 'Ford', model: 'F-150', type: 'truck', price: 27110 },
{ make: 'Ford', model: 'Fusion', type: 'sedan', price: 22120 },
{ make: 'Ford', model: 'Explorer', type: 'suv', price: 31660 }
];
const averageSUVPrice = vehicles
.filter(v => v.type === 'suv')
.map(v => v.price)
.reduce((sum, price, i, array) => sum + price / array.length, 0);
console.log(averageSUVPrice); // 33399
注意我们在一个数组对象上调用其方法,这是面向对象编程的特性。如果我们想要更函数式一些,我们可以用 Rmmda 或者 lodash/fp 提供的函数。注意如果我们使用 R.compose 的话,需要倒转函数的顺序,因为它从右向左依次调用函数(从底向上);然而,如果我们想从左向右调用函数就像上面的例子,我们可以用 R.pipe。下面两个例子用了 Rmmda。注意 Rmmda 有一个 mean 函数用来代替 reduce 。
const vehicles = [
{ make: 'Honda', model: 'CR-V', type: 'suv', price: 24045 },
{ make: 'Honda', model: 'Accord', type: 'sedan', price: 22455 },
{ make: 'Mazda', model: 'Mazda 6', type: 'sedan', price: 24195 },
{ make: 'Mazda', model: 'CX-9', type: 'suv', price: 31520 },
{ make: 'Toyota', model: '4Runner', type: 'suv', price: 34210 },
{ make: 'Toyota', model: 'Sequoia', type: 'suv', price: 45560 },
{ make: 'Toyota', model: 'Tacoma', type: 'truck', price: 24320 },
{ make: 'Ford', model: 'F-150', type: 'truck', price: 27110 },
{ make: 'Ford', model: 'Fusion', type: 'sedan', price: 22120 },
{ make: 'Ford', model: 'Explorer', type: 'suv', price: 31660 }
];
// Using `pipe` executes the functions from top-to-bottom.
const averageSUVPrice1 = R.pipe(
R.filter(v => v.type === 'suv'),
R.map(v => v.price),
R.mean
)(vehicles);
console.log(averageSUVPrice1); // 33399
// Using `compose` executes the functions from bottom-to-top.
const averageSUVPrice2 = R.compose(
R.mean,
R.map(v => v.price),
R.filter(v => v.type === 'suv')
)(vehicles);
console.log(averageSUVPrice2); // 33399
使用函数式方法的优点是清楚地分开了数据(vehicles)和逻辑(函数 filter,map 和 reduce)。面向对象的代码相比之下把数据和函数用以方法的对象的形式混合在了一起。
柯里化
不规范地说,柯里化是把一个接受 n 个参数的函数变成 n 个每个接受单个参数的函数的过程。函数的 arity 是它接受参数的个数。接受一个参数的函数是 unary,两个的是 binary,三个的是 ternary,n 个的是 n-ary。那么,我们可以把柯里化定义成将一个 n-ary 函数转换成 n 个 unary 函数的过程。让我们通过简单的例子开始,一个计算两个向量点积的函数。回忆一下线性代数,两个向量 [a, b, c] 和 [x, y, z] 的点积是 ax + by + cz。
function dot(vector1, vector2) {
return vector1.reduce((sum, element, index) => sum += element * vector2[index], 0);
}
const v1 = [1, 3, -5];
const v2 = [4, -2, -1];
console.log(dot(v1, v2)); // 1(4) + 3(-2) + (-5)(-1) = 4 - 6 + 5 = 3
dot 函数是 binary,因为它接受两个参数;然而我们可以将它手动转换成两个 unary 函数,就像下面的例子。注意 curriedDot 是一个 unary 函数,它接受一个向量并返回另一个接受第二个向量的 unary 函数。
function curriedDot(vector1) {
return function(vector2) {
return vector1.reduce((sum, element, index) => sum += element * vector2[index], 0);
}
}
// Taking the dot product of any vector with [1, 1, 1]
// is equivalent to summing up the elements of the other vector.
const sumElements = curriedDot([1, 1, 1]);
console.log(sumElements([1, 3, -5])); // -1
console.log(sumElements([4, -2, -1])); // 1
很幸运,我们不需要把每一个函数都手动转换成柯里化以后的形式。Ramda 和 lodash 等库可以为我们做这些工作。实际上,它们是柯里化的混合形式。你既可以每次传递一个参数,也可以像原来一样一次传递所有参数。
function dot(vector1, vector2) {
return vector1.reduce((sum, element, index) => sum += element * vector2[index], 0);
}
const v1 = [1, 3, -5];
const v2 = [4, -2, -1];
// Use Ramda to do the currying for us!
const curriedDot = R.curry(dot);
const sumElements = curriedDot([1, 1, 1]);
console.log(sumElements(v1)); // -1
console.log(sumElements(v2)); // 1
// This works! You can still call the curried function with two arguments.
console.log(curriedDot(v1, v2)); // 3
Ramda 和 lodash 都允许你“跳过”一些变量之后再指定它们。它们使用置位符来做这些工作。因为点积的计算可以交换两项。传入向量的顺序不影响结果。让我们换一个例子来阐述如何使用一个置位符。Ramda 使用双下划线作为其置位符。
const giveMe3 = R.curry(function(item1, item2, item3) {
return `
1: ${item1}
2: ${item2}
3: ${item3}
`;
});
const giveMe2 = giveMe3(R.__, R.__, 'French Hens'); // Specify the third argument.
const giveMe1 = giveMe2('Partridge in a Pear Tree'); // This will go in the first slot.
const result = giveMe1('Turtle Doves'); // Finally fill in the second argument.
console.log(result);
// 1: Partridge in a Pear Tree
// 2: Turtle Doves
// 3: French Hens
在我们结束探讨柯里化之前最后的议题是偏函数应用。偏函数应用和柯里化经常同时出场,尽管它们实际上是不同的概念。一个柯里化的函数还是柯里化的函数,即使没有给它任何参数。偏函数应用,另一方面是仅仅给一个函数传递部分参数而不是所有参数。柯里化是偏函数应用常用的方法之一,但是不是唯一的。
JavaScript 拥有一个内置机制可以不依靠柯里化来做偏函数应用。那就是 function.prototype.bind 方法。这个方法的一个特殊之处在于,它要求你将 this 作为第一个参数传入。 如果你不进行面向对象编程,那么你可以通过传入 null 来忽略 this。
1function giveMe3(item1, item2, item3) {
return `
1: ${item1}
2: ${item2}
3: ${item3}
`;
}
const giveMe2 = giveMe3.bind(null, 'rock');
const giveMe1 = giveMe2.bind(null, 'paper');
const result = giveMe1('scissors');
console.log(result);
// 1: rock
// 2: paper
// 3: scissors
总结
我希望你享受探索 JavaScript 中函数式编程的过程。对一些人来说,它可能是一个全新的编程范式,但我希望你能尝试它。你会发现你的程序更易于阅读和调试。不变性还将允许你优化 Angular 和 React 的性能。
这篇文章基于 Matt 在 OpenWest 的演讲 JavaScript the Good-er Parts. OpenWest 将在 6/12-15 ,2017 在 Salt Lake City, Utah 举行。
作者简介:
Matt Banz - Matt 于 2008 年五月在犹他大学获得了数学学位毕业。一个月后他得到了一份 web 开发者的工作,他从那时起就爱上了它!在 2013 年,他在北卡罗莱纳州立大学获得了计算机科学硕士学位。他在 LDS 商学院和戴维斯学区社区教育计划教授 Web 课程。他现在是就职于 Motorola Solutions 公司的高级前端开发者。
via: https://opensource.com/article/17/6/functional-javascript