mirror of
https://github.com/LCTT/TranslateProject.git
synced 2024-12-26 21:30:55 +08:00
291 lines
40 KiB
Markdown
291 lines
40 KiB
Markdown
【Translating by JanzenLiu】
|
||
公钥加密之外
|
||
============================================================
|
||
|
||
关于应用密码学最令人扼腕也最引人入胜的一件事就是*我们在现实中实际使用的密码学是多么的少*。这并不是指密码学在业界没有被广泛的应用————事实上它的应用很广泛。我想指出的是,迄今为止密码学研究人员开发了如此多实用的技术,但工业界平常使用的却少之又少。实际上,除了少数个别情况,我们现今使用的绝大部分密码学技术是在 21 世纪初*就已经存在的技术。
|
||
|
||
大多数人并不在意这点,但作为一个工作在研究与应用之交领域的密码学家,这让我感到不开心。我不能完全解决这个问题,我*能*做的,就是谈论一部分这些新的技术。在这个夏天里,这就是我想要做的:谈论。具体来说,在接下来的几个星期里,我将会写一系列讲述这些前沿而又没被观察到正在被广泛使用的密码学技术的文章。
|
||
|
||
今天我要从一个非常简单的问题开始:在公钥加密之外还有什么(可用的加密技术)?具体地说,我将讨论少量过去20年里开发出的技术,它们让我们可以走出传统的公钥加密的概念的局限。
|
||
|
||
这是一篇专业的技术文章,但是不会有太困难的数学内容。对于涉及方案的实际定义,我会提供一些原论文的链接,以及一些背景知识的参考资料。在这里,我们的关注点是解释这些方案在做什么————以及他们在现实中可以怎样被应用。
|
||
|
||
### 基于身份加密
|
||
|
||
在 20 世纪 80 年代中期,以为名叫 Adi Shamir 的密码学家提出了一个 [全新的想法][3] 。这个想法,简单来说,就是*摒弃公钥*。
|
||
|
||
为了理解 Shamir 的成果从何而来,我们最好先了解一些关于公钥加密的东西。在公钥加密的发明之前,所有的加密技术都牵涉到私钥。处理这样的密钥是相当累赘的工作。在你可以安全地通信之前,你需要和你的伙伴交换密钥。这一过程非常的困难,而且当通信规模增大时不能很好地运作。
|
||
|
||
公钥加密(由 [Diffie-Hellman][4] 和 Shamir 的 [RSA][5] 密码系统发展而来的)通过极大地简化密钥分配的过程给密码学带来了革命性的改变。比起分享私钥,用户现在只要将他们的*公共*密钥发送给其他使用者。有了公共密钥,(密钥的)接收者可以加密给你的信息(或者验证你的数字签名),但是又不能用密钥来进行解密(或者产生数字签名)。这一部分要通过你自己保存的私有密钥来完成。
|
||
|
||
尽管公钥的使用改进了密码学应用的许多方面,它也带来了一系列新的挑战。从实践中的情况来看,拥有公钥往往只是成功的一半————人们通常还需要安全地分发这些公钥。
|
||
|
||
举一个例子,想象一下我想要给你发送一封 PGP 加密的电子邮件。在我可以这么做之前,我需要获得一份你的公钥的拷贝。我要怎么获得呢?显然我们可以亲自会面,然后当面交换这个密钥————但(由于身体会面的麻烦)没有人愿意这样做。通过电子的方式获得你的公钥会更理想。在现实中,这意味着要么*(1)* 我们必须通过电子邮件交换公钥, 要么*(2)* 我必须通过某个第三方基础设施,比如一个 [网站][6] 或者 [密钥服务器][7] ,来获得你的密钥。现在我们面临这样的问题:如果电子邮件或密钥服务器是*不值得信赖的*(或者单纯地允许任何人以 [你的名义][9] [上传密钥][8] ),我就可能会意外下载恶意用户的密钥。当我给“你”发送一条消息的时候,也许我实际上正在将消息加密发送给 Mallory.
|
||
|
||

|
||
Mallory.
|
||
|
||
解决这个问题————关于交换公钥和验证它们的来源的问题————激励了*大量的*实践密码工程,包括整个 [web PKI][10] (网络公钥基础设施)。在大部分情况下,这些系统非常奏效。但是 Shamir 并不满意。如果,他这样问道,我们能做得更好会怎样?更具体地说,他这样思考:*我们是否可以用一些更好的技术去替换那些麻烦的公钥?*
|
||
|
||
Shamir 的想法非常令人激动。他提出的是一个新的公钥加密形式,在这个方案中用户的“公钥”可以就是他们的*身份*。这个身份可以是一个名字(比如“Matt Green”)或者某些诸如电子邮箱地址这样更准确的信息。事实上,“身份”是什么并不重要。重要的是这个公钥可以是一个任意的字符串————而*不是*一大串诸如“ 7cN5K4pspQy3ExZV43F6pQ6nEKiQVg6sBkYPg1FG56Not ”这样无意义的字符组合。
|
||
|
||
当然,使用任意字符串作为公钥会造成一个严重的问题。有意义的身份听起来很棒————但我们无法拥有它们。如果我的公钥是 “Matt Green” ,我要怎么过的对应的私钥。如果*我*能获得那个私钥,又由谁来阻止*其他的某些 Matt Green* 获得同样的私钥,进而读取我的消息。进而考虑一下这个,谁来阻止任意的某个*不是*名为 Matt Green 的人来获得它。啊,我们现在陷入了 [Zooko 三难困境][11] 。
|
||
|
||
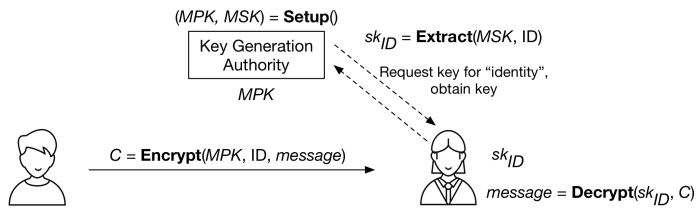
Shamir 的想法因此要求稍微更多一点的手段。相比期望身份可以全世界范围使用,他提出了一个名为“密钥生成机构”的特殊服务器,负责产生私钥。在设立初期,这个机构会产生一个*最高公共密钥(MPK)*,这个公钥将会向全世界公布。如果你想要加密一条消息给“Matt Green”(或者验证我的签名),你可以用我的身份和我们达成一致使用的权威机构的唯一 MPK 来加密。要*解密*这则消息(或者制作签名),我需要访问同一个密钥机构,然后请求一份我的密钥的拷贝。密钥机构将会基于一个秘密保存的 *最高私有密钥(MSK)*来计算我的密钥。
|
||
|
||
加上上述所有的算法和参与者,整个系统看起来是这样的:
|
||
|
||
|
||
一个 基于身份加密(IBE)系统的概览。密钥生成机构的 Setup 算法产生最高公共密钥(MPK)和最高私有密钥(MSK)。机构可以使用 Extract 算法来根据指定的 ID 生成对应的私钥。加密器(左)仅使用身份和 MPK 来加密。消息的接受者请求对应她身份的私钥,然后用这个私钥解密。(图标由 [Eugen Belyakoff][1] 制作)
|
||
|
||
这个设计有一些重要的优点————并且胜过少数明显的缺点。在好的方面,它*完全*摆脱了任何和你发送消息的对象进行密钥交换的必要。一旦你选择了一个主密钥机构(然后下载了它的 MPK),你就可以加密给整个世界上任何一个人的消息。甚至更酷炫地,在你加密的时候,*你的通讯对象甚至还不需要联系密钥机构*。她可以在你给她发送消息*之后*再取得她的私钥。
|
||
|
||
当然,这个“特性”也同时是一个漏洞。因为密钥机构产生所有的私钥,它拥有相当大权力。一个不诚实的机构可以轻易生成你的私钥然后解密你的消息。用更得体的方式来说就是标准的 IBE 系统有效地“包含” [密钥托管机制][12]。**
|
||
|
||
### 基于身份加密(IBE)中的“加密(E)”
|
||
|
||
所有这些想法和额外的思考都是 Shamir 在他 1984 年的论文中提出来的。其中有一个小问题:Shamir 只能解决问题的一半。
|
||
|
||
具体地说,Shamir 提出了一个*基于身份签名(IBS)*的方案————一个公共验证密钥是身份,而签名密钥由密钥机构生成的签名方案。他尽力尝试了,但仍然不能找到一个简历基于身份*加密*的解决方案。这成为了一个公开的问题。***
|
||
|
||
直到有人能解决 Shamir 的难题还有 16 年。令人惊讶的是,当回答出现的时候,它出现了不只一次,*而是三次*。
|
||
|
||
第一个,或许也是最负盛名的 IBE 的实现,是由 Dan Boneh 和 Matthew Franklin 在多年以后开发的。Boneh 和 Franklin 的发现的时机十分有意义。Boneh-Franklin 方案根本上依赖于能支持有效的 [“双线性映射”][13] (或者“配对”)****的椭圆曲线。该类 [算法][14] 需要计算这些配对,而这些配对在 Shamir 撰写他的那篇论文是还不被知晓,因此没有被*建设性地*使用————即被作为比起 [一种攻击][15] 更有用的东西使用————直至 [2000年][16]。第二个被称为 [Sakai-Kasahara][17] 的方案的情况也大抵类似,这个方案将在与第一个大约同一时间被另外一组学者独立发现。
|
||
|
||
*(关于 Boneh-Franklin IBE 方案的简短教学,请查看 [这个页面][2])*
|
||
|
||
第三个 IBE 的实现并不如前二者有效,但却更令人吃惊得多。[这个方案][18] 由 Clifford Cocks,一位英国国家通信总局的资深密码学家开发。它因为两个原因而引人注目。第一,Cocks 的 IBE 方案完全不需要用到双线性映射————都是建立在以往的 RSA 的基础上的,这意味着*原则上*这个算法这么多年来仅仅是没有被人们发现(而非在等待相应的理论基础)而已。第二,Cocks 本人近期因为一些甚至更令人惊奇的东西而闻名:在 RSA 算法被提出之前将近 5 年 [发现 RSA 加密系统][19](即公钥加密算法)。用再一个在公钥加密领域的重要成就来结束这一成就,实在堪称令人印象深刻的创举。
|
||
|
||
自 2001 年起,许多另外的 IBE 构造涌现出来,用到了各种各样的密码学背景知识。尽管如此,Boneh 和 Franklin 早期的实现仍然是这些算法之中最为简单和有效的。
|
||
|
||
即使你并不因为 IBE 自身而对它感兴趣,事实证明它的基本元素对密码学家来说在许许多多单纯地加密之外的领域都十分有用。事实上,如果我们把 IBE 看作是一种由单一的主公/私钥对来产生数以亿计的相关联的密钥对的方式,它将会显得意义非凡。这让 IBE 对于诸如 [选择密文攻击][20], [前向安全的公钥加密][21] 和 [短签名方案][22] 这样各种各样的应用来说非常有用。
|
||
|
||
### 基于特征加密
|
||
|
||
当然,如果你给密码学家以一个类似 IBE 的工具,那么首先他们要做的将是找到一种~~让事情更复杂~~改进它的方法。
|
||
|
||
最大的改进之一要归功于 [Sahai 和 Waters][23]。我们称之为基于特征加密,或者 ABE (Attribute-Based Encryption).
|
||
|
||
这个想法最初并不是为了用特征来加密。相反,Sahai 和 Waters 试图开发一种使用生物辨识特征来加密的*基于身份的*加密方案。为了理解这个问题,想象一下我决定使用某种生物辨识特征,比如你的 [虹膜扫描影像][24],来作为你的“身份”来加密一则给你的密文。然后你将向权威机构请求一个对应你的虹膜的解密密钥————如果一切都匹配得上,你就可以解密信息了。
|
||
|
||
问题就在于这几乎不能奏效。
|
||
|
||
因为生物辨识特征的读取(比如虹膜扫描或者指纹模板)本来就是易出错的。这意味着每一次的读取通常都是十分接近的,但却总是会几个对不上的比特。在标准的 IBE 系统中
|
||
|
||
|
||
告诉我这不会给你带来噩梦
|
||
|
||
这是灾难性的:如果加密使用的身份和你的密钥身份有哪怕是一个比特的不同,解密都会失效。你就不走运了。
|
||
|
||
Sahai 和 Waters 决定通过开发一种包含“阈值门”的 IBE 形式来解决这个问题。在这个背景下,一个身份的每一个字节都被表示为一个不同的“特征”。把每一个这种特征看作是你用于加密的一个元件————譬如“你的虹膜扫描的 5 号字节是 1”和“你的虹膜扫描的 23 号字节是 0”。加密方罗列出所有这些字节,然后将它们中的每一个都用于加密中。权威机构生成的解密密钥也嵌入了一连串相似的字节值。根据这个方案的定义,当且仅当(你的身份密钥与密文解密密钥之间)配对的特征数量超过某个预先定义的阈值时,才能顺利解密:*比如*为了能解密,2048 个字节中的(至少) 2024 个要是对应相同的。
|
||
|
||
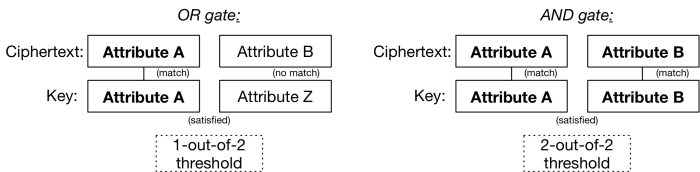
这个想法的优美之处不在于模糊 IBE,在于一旦你有了一个阈值门和一个“特征”的概念,你就能做更有趣的事情。[主要的观察结论][25] 是阈值门可以拥有实现 boolean 的 AND 门和 OR 门(译者认为此处应为用 AND 门和
|
||
OR 门实现, 原文: a threshold gate can be used to implement the boolean AND and OR gates),就像这样:
|
||
|
||
|
||
|
||
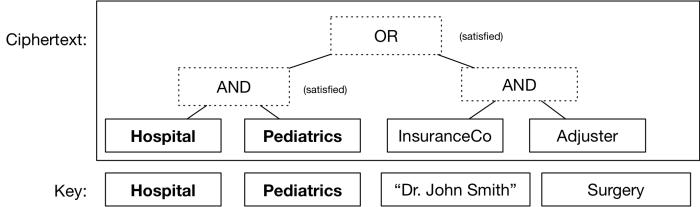
甚至你还可以将这些逻辑闸门*堆叠*起来,一些在另一些之上,来表示一些相当复杂的 boolean 表达式————这些表达式本身就用于判定在什么情况下你的密文可以被解密。举个例子,考虑一组更为现实的特征,你可以这样加密一份医学记录,使医院的儿科医生*或者*保险理算员都可以阅读它。你所需要做的只不过是保证人们可以得到正确描述*他们的*特征的密钥(就是一些任意的字符串,如同身份那样)。
|
||
|
||
|
||
一个简单的“密文规定”。在这个规定中当且仅当一个密钥与一组特定的特征匹配时,密文才能被解密。在这个案例中,密钥满足公式的条件,因此密文将被解密。其余用不到的特征在这里忽略掉。
|
||
|
||
其他的条件判断也能实现。通过一长串特征,比如文件创建时间,文件名,甚至指示文件创建位置的 GPS 坐标, 来加密密文也是有可能的。于是你可以让权威机构分发一部分对应你的数据集非常精确的一部分的密钥————比如说,“该密钥用于解密所有在 11 月 3 号和 12 月 12 号之间在芝加哥被加密的包含‘小儿科’或者‘肿瘤科’标记的放射科文件”。
|
||
|
||
### 函数式加密
|
||
|
||
一旦拥有一个相关的基础工具,像 IBE 和 ABE,研究人员的本能是去扩充和一般化它。为什么要止步于简单的 boolean 表达式?我们能不能制作嵌入了*任意的计算机程序*的密钥(或者密文)?答案被证明是肯定的————尽管不是非常高效。一组 [近几年的][26] [研究][27] 显示可以根据各种各样的基于格的密码假设,构建在任意多项式大小线路运作的 ABE。所以这一方向毫无疑问非常有发展潜力。
|
||
|
||
这一潜力启发了研究人员将所有以上的想法一般化成为一个被称作 “[函数式加密]” 的单独的类。函数式加密更多是一种抽象的概念而没有具体所指————它不过是一种将所有这些系统看作是一个特定的累的实例的方式。它基本的想法是,
|
||
This potential has inspired researchers to generalize all of the above ideas into a single class of encryption called “[functional encryption][28]“. Functional encryption is more conceptual than concrete — it’s just a way to look at all of these systems as instances of a specific class. The basic idea is to represent the decryption procedure as an algorithm that computes an arbitary function _F_ over (1) the plaintext inside of a ciphertext, and (2) the data embedded in the key. This function has the following profile:
|
||
|
||
_output = F(key data, plaintext data)_
|
||
|
||
In this model _IBE_ can be expressed by having the encryption algorithm encrypt _ (identity, plaintext) _ and defining the function _F _ such that, if “ _key input == identity”, it _ outputs the plaintext, and outputs an empty string otherwise. Similarly, ABE can be expressed by a slightly more complex function. Following this paradigm, once can envision all sorts of interesting functions that might be computed by different functions and realized by future schemes.
|
||
|
||
But those will have to wait for another time. We’ve gone far enough for today.
|
||
|
||
### So what’s the point of all this?
|
||
|
||
For me, the point is just to show that cryptography can do some pretty amazing things. We rarely see this on a day-to-day basis when it comes to industry and “applied” cryptography, but it’s all there waiting to be used.
|
||
|
||
Perhaps the perfect application is out there. Maybe you’ll find it.
|
||
|
||
_Notes:_
|
||
|
||
* An earlier version of this post said “mid-1990s”. In comments below, Tom Ristenpart takes issue with that and makes the excellent point that many important developments post-date that. So I’ve moved the date forward about five years, and I’m thinking about how to say this in a nicer way.
|
||
|
||
** There is also an intermediate form of encryption known as “[certificateless encryption][29]“. Proposed by Al-Riyami and Paterson, this idea uses a _combination_ of standard public key encryption and IBE. The basic idea is to encrypt each message using _both_ a traditional public key (generated by the recipient) and an IBE identity. The recipient must then obtain a copy of the secret key from the IBE authority to decrypt. The advantages here are twofold: (1) the IBE key authority can’t decrypt the message by itself, since it does not have the corresponding secret key, which solves the “escrow” problem. And (2) the sender does not need to verify that the public key really belongs to the sender (e.g., by checking a certificate), since the IBE portion prevents imposters from decrypting the resulting message. Unfortunately this system is more like traditional public key cryptography than IBE, and does not have the neat usability features of IBE.
|
||
|
||
*** A part of the challenge of developing IBE is the need to make a system that is secure against “collusion” between different key holders. For example, imagine a very simple system that has only 2-bit identities. This gives four possible identities: “00”, “01”, “10”, “11”. If I give you a key for the identity “01” and I give Bob a key for “10”, we need to ensure that you two cannot collude to produce a key for identities “00” and “11”. Many earlier proposed solutions have tried to solve this problem by gluing together standard public encryption keys in various ways (e.g., by having a separate public key for each bit of the identity and giving out the secret keys as a single “key”). However these systems tend to fail catastrophically when just a few users collude (or their keys are stolen). Solving the collusion problem is fundamentally what separates real IBE from its faux cousins.
|
||
|
||
**** A full description of Boneh and Franklin’s scheme can be found [here][30], or in the [original paper][31]. Some code is [here][32] and [here][33] and [here][34]. I won’t spend more time on it, except to note that the scheme is very efficient. It was patented and implemented by [Voltage Security][35], now part of HPE.
|
||
|
||
--------------------------------------------------------------------------------
|
||
|
||
via: https://github.com/LCTT/TranslateProject/tree/master/sources/tech
|
||
|
||
作者:[Matthew Green][a]
|
||
译者:[Janzen_Liu](https://github.com/JanzenLiu)
|
||
校对:[校对者ID](https://github.com/校对者ID)
|
||
|
||
本文由 [LCTT](https://github.com/LCTT/TranslateProject) 原创编译,[Linux中国](https://linux.cn/) 荣誉推出
|
||
|
||
--------------------------------------------------------------------------------
|
||
【原文】Beyond public key encryption
|
||
============================================================
|
||
|
||
One of the saddest and most fascinating things about applied cryptography is _how
|
||

|
||
little cryptography we actually use. _ This is not to say that cryptography isn’t widely used in industry — it is. Rather, what I mean is that cryptographic researchers have developed so many useful technologies, and yet industry on a day to day basis barely uses any of them. In fact, with a few minor exceptions, the vast majority of the cryptography we use was settled by the early-2000s.*
|
||
|
||
Most people don’t sweat this, but as a cryptographer who works on the boundary of research and deployed cryptography it makes me unhappy. So while I can’t solve the problem entirely, what I _can_ do is talk about some of these newer technologies. And over the course of this summer that’s what I intend to do: talk. Specifically, in the next few weeks I’m going to write a series of posts that describe some of the advanced cryptography that we _don’t_ generally see used.
|
||
|
||
Today I’m going to start with a very simple question: what lies beyond public key cryptography? Specifically, I’m going to talk about a handful of technologies that were developed in the past 20 years, each of which allows us to go beyond the traditional notion of public keys.
|
||
|
||
This is a wonky post, but it won’t be mathematically-intense. For actual definitions of the schemes, I’ll provide links to the original papers, and references to cover some of the background. The point here is to explain what these new schemes do — and how they can be useful in practice.
|
||
|
||
### Identity Based Cryptography
|
||
|
||
In the mid-1980s, a cryptographer named Adi Shamir proposed a [radical new idea.][3]The idea, put simply, was _to get rid of public keys_ .
|
||
|
||
To understand where Shamir was coming from, it helps to understand a bit about public key encryption. You see, prior to the invention of public key crypto, all cryptography involved secret keys. Dealing with such keys was a huge drag. Before you could communicate securely, you needed to exchange a secret with your partner. This process was fraught with difficulty and didn’t scale well.
|
||
|
||
Public key encryption (beginning with [Diffie-Hellman][4] and Shamir’s [RSA][5]cryptosystem) hugely revolutionized cryptography by dramatically simplifying this key distribution process. Rather than sharing secret keys, users could now transmit their _public_ key to other parties. This public key allowed the recipient to encrypt to you (or verify your signature) but it could not be used to perform the corresponding decryption (or signature generation) operations. That part would be done with a secret key you kept to yourself.
|
||
|
||
While the use of public keys improved many aspects of using cryptography, it also gave rise to a set of new challenges. In practice, it turns out that having public keys is only half the battle — people still need to use distribute them securely.
|
||
|
||
For example, imagine that I want to send you a PGP-encrypted email. Before I can do this, I need to obtain a copy of your public key. How do I get this? Obviously we could meet in person and exchange that key on physical media — but nobody wants to do this. It would much more desirable to obtain your public key electronically. In practice this means either _(1)_ we have to exchange public keys by email, or _(2)_ I have to obtain your key from a third piece of infrastructure, such as a [website][6] or [key server][7]. And now we come to the problem: if that email or key server is _untrustworthy _ (or simply allows anyone to [upload a key in y][8][our name][9]),I might end up downloading a malicious party’s key by accident. When I send a message to “you”, I’d actually be encrypting it to Mallory.
|
||
|
||

|
||
Mallory.
|
||
|
||
Solving this problem — of exchanging public keys and verifying their provenance — has motivated a _huge_ amount of practical cryptographic engineering, including the entire [web PKI.][10] In most cases, these systems work well. But Shamir wasn’t satisfied. What if, he asked, we could do it better? More specifically, he asked: _could we replace those pesky public keys with something better?_
|
||
|
||
Shamir’s idea was exciting. What he proposed was a new form of public key cryptography in which the user’s “public key” could simply be their _identity_ . This identity could be a name (e.g., “Matt Green”) or something more precise like an email address. Actually, it didn’t realy matter. What did matter was that the public key would be some arbitrary string — and _not_ a big meaningless jumble of characters like “7cN5K4pspQy3ExZV43F6pQ6nEKiQVg6sBkYPg1FG56Not”.
|
||
|
||
Of course, using an arbitrary string as a public key raises a big problem. Meaningful identities sound great — but I don’t own them. If my public key is “Matt Green”, how do I get the corresponding private key? And if _I_ can get out that private key, what stops _some other Matt Green_ from doing the same, and thus reading my messages? And ok, now that I think about this, what stops some random person who _isn’t_ named Matt Green from obtaining it? Yikes. We’re headed straight into [Zooko’s triangle][11].
|
||
|
||
Shamir’s idea thus requires a bit more finesse. Rather than expecting identities to be global, he proposed a special server called a “key generation authority” that would be responsible for generating the private keys. At setup time, this authority would generate a single _master public key (MPK), _ which it would publish to the world. If you wanted to encrypt a message to “Matt Green” (or verify my signature), then you could do so using my identity and the single MPK of an authority we’d both agree to use. To _decrypt _ that message (or sign one), I would have to visit the same key authority and ask for a copy of my secret key. The key authority would compute my key based on a _master secret key (MSK)_ , which it would keep very secret.
|
||
|
||
With all algorithms and players specified, whole system looks like this:
|
||
|
||

|
||
Overview of an Identity-Based Encryption (IBE) system. The Setup algorithm of the Key Generation Authority generates the master public key (MPK) and master secret key (MSK). The authority can use the Extract algorithm to derive the secret key corresponding to a specific ID. The encryptor (left) encrypts using only the identity and MPK. The recipient requests the secret key for her identity, and then uses it to decrypt. (Icons by [Eugen Belyakoff][1])
|
||
|
||
This design has some important advantages — and more than a few obvious drawbacks. On the plus side, it removes the need for any key exchange _at all_ with the person you’re sending the message to. Once you’ve chosen a master key authority (and downloaded its MPK), you can encrypt to anyone in the entire world. Even cooler: at the time you encrypt, _your recipient doesn’t even need to have contacted the key authority yet_ . She can obtain her secret key _after_ I send her a message.
|
||
|
||
Of course, this “feature” is also a bug. Because the key authority generates all the secret keys, it has an awful lot of power. A dishonest authority could easily generate your secret key and decrypt your messages. The polite way to say this is that standard IBE systems effectively “bake in” [key escrow][12].**
|
||
|
||
### Putting the “E” in IBE
|
||
|
||
All of these ideas and more were laid out by Shamir in his 1984 paper. There was just one small problem: Shamir could only figure out half the problem.
|
||
|
||
Specifically, Shamir’s proposed a scheme for _identity-based signature_ (IBS) — a signature scheme where the public verification key is an identity, but the signing key is generated by the key authority. Try as he might, he could not find a solution to the problem of building identity-based _ encryption _ (IBE). This was left as an open problem.***
|
||
|
||
It would take more than 16 years before someone answered Shamir’s challenge. Surprisingly, when the answer came it came not once _but three times_ .
|
||
|
||
The first, and probably most famous realization of IBE was developed by Dan Boneh and Matthew Franklin much later — in 2001\. The timing of Boneh and Franklin’s discovery makes a great deal of sense. The Boneh-Franklin scheme relies fundamentally on elliptic curves that support an efficient “[bilinear map][13]” (or “pairing”).**** The [algorithms][14] needed to compute such pairings were not known when Shamir wrote his paper, and weren’t employed _constructively_ — that is, as a useful thing rather than [an attack][15] — until about [2000][16]. The same can be said about a second scheme called [Sakai-Kasahara][17], which would be independently discovered around the same time.
|
||
|
||
_(For a brief tutorial on the Boneh-Franklin IBE scheme, see [this page][2].)_
|
||
|
||
The third realization of IBE was not as efficient as the others, but was much more surprising. [This scheme][18] was developed by Clifford Cocks, a senior cryptologist at Britain’s GCHQ. It’s noteworthy for two reasons. First, Cocks’ IBE scheme does not require bilinear pairings at all — it is based in the much older RSA setting, which means _in principle _ it spent all those years just waiting to be found. Second, Cocks himself had recently become known for something even more surprising: [discovering the RSA cryptosystem,][19] nearly five years before RSA did. To bookend that accomplishment with a second major advance in public key cryptography was a pretty impressive accomplishment.
|
||
|
||
In the years since 2001, a number of additional IBE constructions have been developed, using all sorts of cryptographic settings. Nonetheless, Boneh and Franklin’s early construction remains among the simplest and most efficient.
|
||
|
||
Even if you’re not interested in IBE for its own sake, it turns out that this primitive is really useful to cryptographers for many things beyond simple encryption. In fact, it’s more helpful to think of IBE as a way of “pluralizing” a single public/secret master keypair into billions of related keypairs. This makes it useful for applications as diverse as blocking [chosen ciphertext attacks,][20] [forward-secure public key encryption][21], and short [signature schemes][22].
|
||
|
||
Attribute Based Encryption
|
||
|
||
Of course, if you leave cryptographers alone with a tool like IBE, the first thing they’re going to do is find a way to ~~make things more complicated~~ improve on it.
|
||
|
||
One of the biggest such improvements is due to [Sahai and Waters][23]. It’s called Attribute-Based Encryption, or ABE.
|
||
|
||
The origin of this idea was not actually to encrypt with attributes. Instead Sahai and Waters were attempting to develop an _Identity-Based_ encryption scheme that could encrypt using biometrics. To understand the problem, imagine I decide to use a biometric like your [iris scan][24] as the “identity” to encrypt you a ciphertext. Later on you’ll ask the authority for a decryption key that corresponds to your own iris scan — and if everything matches up and you’ll be able to decrypt.
|
||
|
||
The problem is that this will almost never work.
|
||
|
||
The issue here is that biometric readings (like iris scans or fingerprint templates) are inherently error-prone. This means every scan will typically be very _close_ , but often there will be a few bits that disagree. With standard IBE
|
||
|
||

|
||
Tell me this isn’t giving you nightmares.
|
||
|
||
this is _fatal_ : if the encryption identity differs from your key identity by even a single bit, decryption will not work. You’re out of luck.
|
||
|
||
Sahai and Waters decided that the solution to this problem was to develop a form of IBE with a “threshold gate”. In this setting, each bit of the identity is represented as a different “attribute”. Think of each of these as components you’d encrypt under — something like “bit 5 of your iris scan is a 1” and “bit 23 of your iris scan is a 0”. The encrypting party lists all of these bits and encrypts under each one. The decryption key generated by the authority embeds a similar list of bit values. The scheme is defined so that decryption will work if and only if the number of matching attributes (between your key and the ciphertext) exceeds some pre-defined threshold: _e.g.,_ any 2024 out of 2048 bits must be identical in order to decrypt.
|
||
|
||
The beautiful thing about this idea is not fuzzy IBE. It’s that once you have a threshold gate and a concept of “attributes”, you can more interesting things. The [main observation][25] is that a threshold gate can be used to implement the boolean AND and OR gates, like so:
|
||
|
||

|
||
|
||
Even better, you can _stack_ these gates on top of one another to assign a fairly complex boolean formula — which will itself determine what conditions your ciphertext can be decrypted under. For example, switching to a more realistic set of attributes, you could encrypt a medical record so that either a pediatrician in a hospital could read it, _or_ an insurance adjuster could. All you’d need is to make sure people received keys that correctly described _their_ attributes (which are just arbitrary strings, like identities).
|
||
|
||

|
||
A simple “ciphertext policy”, in which the ciphertext can be decrypted if and only if a key matches an appropriate set of attributes. In this case, the key satisfies the formula and thus the ciphertext decrypts. The remaining key attributes are ignored.
|
||
|
||
The other direction can be implemented as well. It’s possible to encrypt a ciphertext under a long list of attributes, such as creation time, file name, and even GPS coordinates indicating where the file was created. You can then have the authority hand out keys that correspond to a very precise slice of your dataset — for example, “this key decrypts any radiology file encrypted in Chicago between November 3rd and December 12th that is tagged with ‘pediatrics’ or ‘oncology'”.
|
||
|
||
### Functional Encryption
|
||
|
||
Once you have a related of primitives like IBE and ABE, the researchers’ instinct is to both extend and generalize. Why stop at simple boolean formulae? Can we make keys (or ciphertexts) that embed _arbitrary computer programs? _ The answer, it turns out, is yes — though not terribly efficiently. A set of [recent][26] [works][27] show that it is possible to build ABE that works over arbitrary polynomial-size circuits, using various lattice-based assumptions. So there is certainly a lot of potential here.
|
||
|
||
This potential has inspired researchers to generalize all of the above ideas into a single class of encryption called “[functional encryption][28]“. Functional encryption is more conceptual than concrete — it’s just a way to look at all of these systems as instances of a specific class. The basic idea is to represent the decryption procedure as an algorithm that computes an arbitary function _F_ over (1) the plaintext inside of a ciphertext, and (2) the data embedded in the key. This function has the following profile:
|
||
|
||
_output = F(key data, plaintext data)_
|
||
|
||
In this model _IBE_ can be expressed by having the encryption algorithm encrypt _ (identity, plaintext) _ and defining the function _F _ such that, if “ _key input == identity”, it _ outputs the plaintext, and outputs an empty string otherwise. Similarly, ABE can be expressed by a slightly more complex function. Following this paradigm, once can envision all sorts of interesting functions that might be computed by different functions and realized by future schemes.
|
||
|
||
But those will have to wait for another time. We’ve gone far enough for today.
|
||
|
||
### So what’s the point of all this?
|
||
|
||
For me, the point is just to show that cryptography can do some pretty amazing things. We rarely see this on a day-to-day basis when it comes to industry and “applied” cryptography, but it’s all there waiting to be used.
|
||
|
||
Perhaps the perfect application is out there. Maybe you’ll find it.
|
||
|
||
_Notes:_
|
||
|
||
* An earlier version of this post said “mid-1990s”. In comments below, Tom Ristenpart takes issue with that and makes the excellent point that many important developments post-date that. So I’ve moved the date forward about five years, and I’m thinking about how to say this in a nicer way.
|
||
|
||
** There is also an intermediate form of encryption known as “[certificateless encryption][29]“. Proposed by Al-Riyami and Paterson, this idea uses a _combination_ of standard public key encryption and IBE. The basic idea is to encrypt each message using _both_ a traditional public key (generated by the recipient) and an IBE identity. The recipient must then obtain a copy of the secret key from the IBE authority to decrypt. The advantages here are twofold: (1) the IBE key authority can’t decrypt the message by itself, since it does not have the corresponding secret key, which solves the “escrow” problem. And (2) the sender does not need to verify that the public key really belongs to the sender (e.g., by checking a certificate), since the IBE portion prevents imposters from decrypting the resulting message. Unfortunately this system is more like traditional public key cryptography than IBE, and does not have the neat usability features of IBE.
|
||
|
||
*** A part of the challenge of developing IBE is the need to make a system that is secure against “collusion” between different key holders. For example, imagine a very simple system that has only 2-bit identities. This gives four possible identities: “00”, “01”, “10”, “11”. If I give you a key for the identity “01” and I give Bob a key for “10”, we need to ensure that you two cannot collude to produce a key for identities “00” and “11”. Many earlier proposed solutions have tried to solve this problem by gluing together standard public encryption keys in various ways (e.g., by having a separate public key for each bit of the identity and giving out the secret keys as a single “key”). However these systems tend to fail catastrophically when just a few users collude (or their keys are stolen). Solving the collusion problem is fundamentally what separates real IBE from its faux cousins.
|
||
|
||
**** A full description of Boneh and Franklin’s scheme can be found [here][30], or in the [original paper][31]. Some code is [here][32] and [here][33] and [here][34]. I won’t spend more time on it, except to note that the scheme is very efficient. It was patented and implemented by [Voltage Security][35], now part of HPE.
|
||
|
||
[a]:https://blog.cryptographyengineering.com/author/matthewdgreen/
|
||
[1]:https://thenounproject.com/eugen.belyakoff/
|
||
[2]:https://blog.cryptographyengineering.com/boneh-franklin-ibe/
|
||
[3]:https://discovery.csc.ncsu.edu/Courses/csc774-S08/reading-assignments/shamir84.pdf
|
||
[4]:https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange
|
||
[5]:https://en.wikipedia.org/wiki/RSA_(cryptosystem)
|
||
[6]:https://keybase.io/
|
||
[7]:https://pgp.mit.edu/
|
||
[8]:https://motherboard.vice.com/en_us/article/bmvdwd/wave-of-spoofed-encryption-keys-shows-weakness-in-pgp
|
||
[9]:https://motherboard.vice.com/en_us/article/bmvdwd/wave-of-spoofed-encryption-keys-shows-weakness-in-pgp
|
||
[10]:https://en.wikipedia.org/wiki/Certificate_authority
|
||
[11]:https://en.wikipedia.org/wiki/Zooko%27s_triangle
|
||
[12]:https://en.wikipedia.org/wiki/Key_escrow
|
||
[13]:http://people.csail.mit.edu/alinush/6.857-spring-2015/papers/bilinear-maps.pdf
|
||
[14]:https://crypto.stanford.edu/miller/
|
||
[15]:http://ieeexplore.ieee.org/document/259647/
|
||
[16]:https://pdfs.semanticscholar.org/845e/96c20e5a5ff3b03f4caf72c3cb817a7fa542.pdf
|
||
[17]:https://en.wikipedia.org/wiki/Sakai%E2%80%93Kasahara_scheme
|
||
[18]:https://pdfs.semanticscholar.org/8289/821325781e2f0ce83cfbfc1b62c44be799ee.pdf
|
||
[19]:https://cryptome.org/jya/ellisdoc.htm
|
||
[20]:https://www.cs.umd.edu/~jkatz/papers/id-cca.pdf
|
||
[21]:https://eprint.iacr.org/2003/083.pdf
|
||
[22]:https://en.wikipedia.org/wiki/Boneh%E2%80%93Lynn%E2%80%93Shacham
|
||
[23]:https://eprint.iacr.org/2004/086.pdf
|
||
[24]:https://en.wikipedia.org/wiki/Iris_recognition
|
||
[25]:https://eprint.iacr.org/2006/309.pdf
|
||
[26]:https://eprint.iacr.org/2013/337.pdf
|
||
[27]:https://arxiv.org/abs/1210.5287
|
||
[28]:https://eprint.iacr.org/2010/543.pdf
|
||
[29]:http://eprint.iacr.org/2003/126.pdf
|
||
[30]:https://en.wikipedia.org/wiki/Boneh%E2%80%93Franklin_scheme
|
||
[31]:https://crypto.stanford.edu/~dabo/papers/bfibe.pdf
|
||
[32]:http://go-search.org/view?id=github.com%2Fvanadium%2Fgo.lib%2Fibe
|
||
[33]:https://github.com/relic-toolkit/relic
|
||
[34]:https://github.com/JHUISI/charm
|
||
[35]:https://www.voltage.com/
|