mirror of
https://github.com/LCTT/TranslateProject.git
synced 2025-01-13 22:30:37 +08:00
148 lines
8.5 KiB
Markdown
148 lines
8.5 KiB
Markdown
|
|
如何在 Python 中写你喜爱的 R 函数
|
|||
|
|
======
|
|||
|
|
R 还是 Python ? 这个 Python 脚本模仿方便的 R 风格函数,使统计数据变得简单易行。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
“Python vs. R” 是数据科学和机器学习的现代战争之一。毫无疑问,近年来两者发展迅猛并成为数据科学,预测分析和机器学习领域的顶级编程语言。事实上,根据 IEEE 最近一篇文章,Python 已在 [最受欢迎编程语言排行榜][1] 中超越 C++ 并且 R 语言也稳居前 10 位。
|
|||
|
|
|
|||
|
|
但是,这两者之间存在一些根本区别。[R] 主要作为统计分析和数据分析问题的快速原型设计的工具而开发的。另一方面,Python 开发为一种通用的,现代的面向对象语言,类似 C++ 或 Java,但具有更简单的学习曲线和更灵活的语言风格。因此,R 仍在统计学家,定量生物学家,物理学家和经济学家中备受青睐,而 Python 已逐渐成为日常脚本,自动化,后端Web开发,分析和通用机器学习框架的顶级语言并拥有广泛的支持基础和开源开发社区。
|
|||
|
|
|
|||
|
|
###在 Python 环境中模仿函数式编程
|
|||
|
|
|
|||
|
|
[R] 作为函数式编程语言的天性为用户提供了一个极其简单和紧凑的借口,用于快速计算概率和数据分析问题的基本描述/推论统计。例如,只用一个紧凑的函数调用来解决以下问题难道不是很好吗?
|
|||
|
|
|
|||
|
|
* 如何计算数据向量的均值 / 中值 / 众数。
|
|||
|
|
* 如何计算某些服从正态分布事件的累积概率。如果服从 Poisson 分布会怎样?
|
|||
|
|
* 如何计算一系列数据点的四分差。
|
|||
|
|
* 如何生成服从学生 t 分布的一些随机数。
|
|||
|
|
|
|||
|
|
R编程环境可以完成所有这些工作。
|
|||
|
|
|
|||
|
|
另一方面,Python的脚本编写能力使分析师能够在各种分析流程中使用这些统计数据,具有无限的复杂性和创造力。
|
|||
|
|
|
|||
|
|
要结合二者的优势,您只需要一个简单的基于 Python 的包装器库,其中包含与 R 风格定义的概率分布和描述性统计相关的最常用函数。 这使您可以非常快速地调用这些函数,而无需转到正确的 Python 统计库并理解整个方法和参数列表。
|
|||
|
|
|
|||
|
|
|
|||
|
|
### 便于调用 R 函数的 Python 包装脚本
|
|||
|
|
|
|||
|
|
[我编写了一个Python脚本] [4] 在 Python 中定义了简单统计分析中方便广泛使用的 R 函数。
|
|||
|
|
|
|||
|
|
此脚本的目标是提供简单的 Python 子例程,模仿 R 风格的统计函数,以快速计算密度/点估计,累积分布和分位数,并生成重要概率分布的随机变量。
|
|||
|
|
|
|||
|
|
为了保持 R 风格的精髓,脚本不使用类层次结构,并且只在文件中定义原始函数。 因此,用户可以导入这个 Python 脚本,并在需要单个名称调用时使用所有功能。
|
|||
|
|
|
|||
|
|
请注意,我使用 mimic 这个词。 在任何情况下,我都声称要模仿 R 的真正的函数式编程范例,该范式包括深层环境设置以及这些环境和对象之间的复杂关系。 这个脚本允许我(我希望无数其他 Python 用户)快速启动P ython 程序或 Jupyter 笔记本,导入脚本,并立即开始进行简单的描述性统计。 这就是目标,仅此而已。
|
|||
|
|
|
|||
|
|
如果您已经写过 R 代码(可能在研究生院)并且刚刚开始学习并使用 Python 进行数据分析,那么您将很高兴看到并在 Jupyter 笔记本中以类似在 R 环境中一样使用一些相同的知名函数。
|
|||
|
|
|
|||
|
|
无论出于何种原因,使用这个脚本很有趣。
|
|||
|
|
|
|||
|
|
### 简单的例子
|
|||
|
|
|
|||
|
|
首先,只需导入脚本并开始处理数字列表,就好像它们是 R 中的数据向量一样。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
from R_functions import *
|
|||
|
|
lst=[20,12,16,32,27,65,44,45,22,18]
|
|||
|
|
<more code, more statistics...>
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
假设您想从数据点向量计算[Tuckey五数] [5]摘要。 你只需要调用一个简单的函数 ** fivenum **,然后传递向量。 它将返回 NumPy 数组中的五数摘要。
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
lst=[20,12,16,32,27,65,44,45,22,18]
|
|||
|
|
fivenum(lst)
|
|||
|
|
> array([12. , 18.5, 24.5, 41. , 65. ])
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
或许你想要知道下面问题的解答
|
|||
|
|
|
|||
|
|
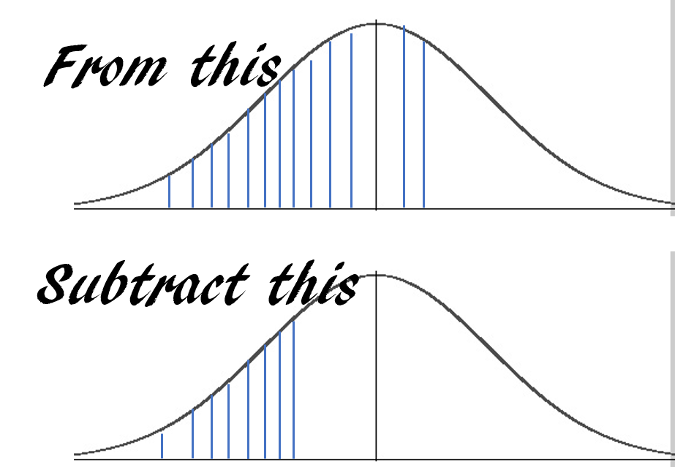
假设一台机器平均每小时输出 10 件成品,标准偏差为 2。输出模式遵循接近正态的分布。 机器在下一个小时内输出至少 7 个但不超过 12 个单位的概率是多少?
|
|||
|
|
|
|||
|
|
答案基本上是这样的:
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
您可以使用 **pnorm** 只用一行代码获得答案:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
pnorm(12,10,2)-pnorm(7,10,2)
|
|||
|
|
> 0.7745375447996848
|
|||
|
|
```
|
|||
|
|
或者您可能需要回答以下问题:
|
|||
|
|
|
|||
|
|
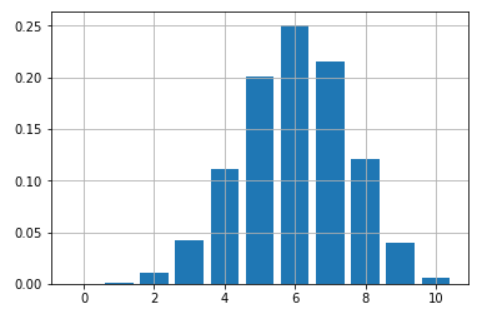
假设你有一个不正的硬币,每次投它时有 60% 可能正面朝上。 你正在玩10次投掷游戏。 你如何绘制并给出这枚硬币所有可能的胜利数(从0到10)?
|
|||
|
|
|
|||
|
|
只需使用一个函数 **dbinom** 就可以获得一个只有几行代码的漂亮条形图:
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
probs=[]
|
|||
|
|
import matplotlib.pyplot as plt
|
|||
|
|
for i in range(11):
|
|||
|
|
probs.append(dbinom(i,10,0.6))
|
|||
|
|
plt.bar(range(11),height=probs)
|
|||
|
|
plt.grid(True)
|
|||
|
|
plt.show()
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
### 简单概率计算接口
|
|||
|
|
|
|||
|
|
R 提供了一个非常简单直观的界面,可以从基本概率分布中快速计算。 接口如下:
|
|||
|
|
|
|||
|
|
* **d** {distribution} 给出点 **x** 处的密度函数值
|
|||
|
|
* **p** {distribution} 给出 **x**点的累积值
|
|||
|
|
* **q** {distribution} 以概率 **p**给出分位数函数值
|
|||
|
|
* **r** {distribution} 生成一个或多个随机变量
|
|||
|
|
|
|||
|
|
在我们的实现中,我们坚持使用此接口及其关联的参数列表,以便您可以像在 R 环境中一样执行这些函数。
|
|||
|
|
|
|||
|
|
### 目前实现的函数
|
|||
|
|
|
|||
|
|
脚本中实现了以下R风格函数,以便快速调用。
|
|||
|
|
|
|||
|
|
* 均值,中位数,方差,标准差
|
|||
|
|
* Tuckey 五数总结,IQR
|
|||
|
|
* 矩阵的协方差或两个向量之间的协方差
|
|||
|
|
* 以下分布的密度,累积概率,分位数函数和随机变量生成:正态,均匀,二项式,泊松,F,学生t,卡方,β和伽马
|
|||
|
|
|
|||
|
|
### 进行中的工作
|
|||
|
|
|
|||
|
|
显然,这是一项正在进行的工作,我计划在此脚本中添加一些其他方便的R函数。 例如,在 R 中,单行命令 ** lm ** 可以为数字数据集提供一个普通的最小二乘拟合模型,其中包含所有必要的推理统计量(P 值,标准误差等)。 这是有力的简洁和紧凑! 另一方面,Python 中的标准线性回归问题经常使用 [Scikit-learn] [6] 来处理,这需要更多的脚本用于此用途,所以我打算使用 Python 的 [statsmodels] 合并这个单函数线性模型拟合特征 [7]后端。
|
|||
|
|
|
|||
|
|
如果您喜欢并在工作中使用此脚本,请通过主演或分析其 [GitHub存储库] [8]帮助其他人找到它。 另外,您可以查看我的其他 [GitHub repos] [9],了解 Python,R 或 MATLAB 中的有趣代码片段以及一些机器学习资源。
|
|||
|
|
|
|||
|
|
如果您有任何问题或想法要分享,请通过 [tirthajyoti [AT] gmail.com] [10]与我联系。 如果你像我一样热衷于机器学习和数据科学,请 [加我在LinkedIn] [11]或[在Twitter上关注我。] [12]
|
|||
|
|
|
|||
|
|
最初发表于[走向数据科学] [13]。 转载于[CC BY-SA 4.0] [14]。
|
|||
|
|
|
|||
|
|
--------------------------------------------------------------------------------
|
|||
|
|
|
|||
|
|
via: https://opensource.com/article/18/10/write-favorite-r-functions-python
|
|||
|
|
|
|||
|
|
作者:[Tirthajyoti Sarkar][a]
|
|||
|
|
选题:[lujun9972][b]
|
|||
|
|
译者:[yongshouzhang](https://github.com/yongshouzhang)
|
|||
|
|
校对:[校对者ID](https://github.com/校对者ID)
|
|||
|
|
|
|||
|
|
本文由 [LCTT](https://github.com/LCTT/TranslateProject) 原创编译,[Linux中国](https://linux.cn/) 荣誉推出
|
|||
|
|
|
|||
|
|
[a]: https://opensource.com/users/tirthajyoti
|
|||
|
|
[b]: https://github.com/lujun9972
|
|||
|
|
[1]: https://spectrum.ieee.org/at-work/innovation/the-2018-top-programming-languages
|
|||
|
|
[2]: https://www.coursera.org/lecture/r-programming/overview-and-history-of-r-pAbaE
|
|||
|
|
[3]: http://adv-r.had.co.nz/Functional-programming.html
|
|||
|
|
[4]: https://github.com/tirthajyoti/StatsUsingPython/blob/master/R_Functions.py
|
|||
|
|
[5]: https://en.wikipedia.org/wiki/Five-number_summary
|
|||
|
|
[6]: http://scikit-learn.org/stable/
|
|||
|
|
[7]: https://www.statsmodels.org/stable/index.html
|
|||
|
|
[8]: https://github.com/tirthajyoti/StatsUsingPython
|
|||
|
|
[9]: https://github.com/tirthajyoti?tab=repositories
|
|||
|
|
[10]: mailto:tirthajyoti@gmail.com
|
|||
|
|
[11]: https://www.linkedin.com/in/tirthajyoti-sarkar-2127aa7/
|
|||
|
|
[12]: https://twitter.com/tirthajyotiS
|
|||
|
|
[13]: https://towardsdatascience.com/how-to-write-your-favorite-r-functions-in-python-11e1e9c29089
|
|||
|
|
[14]: https://creativecommons.org/licenses/by-sa/4.0/
|